Une étoile est fondamentalement un système hors-équilibre qui devrait être modélisé par des équations hydrodynamiques décrivant le transport de matière et d’énergie. Nous allons adopter ici une approche hydrostatique plus simple, qui suffit à rendre compte qualitativement, et souvent même quantitativement des propriétés d’une étoile. Nous allons supposer que l’étoile est une sphère isotrope dans laquelle la matière et le rayonnement – bien que globalement hors-équilibre – sont localement à l’équilibre thermodynamique et peuvent donc être caractérisés par une pression \(P(r)\) et une température \(T(r)\) liées par l’équation d’état des gaz parfaits (pour la matière) et la loi de Stefan-Boltzmann (pour les photons).
Dans les conditions de température qui règnent à l’intérieur une étoile, la plupart des atomes sont complètement ionisés1, si bien que noyaux et électrons forment un plasma que l’on supposera classique (non dégénéré, non relativiste). Ce plasma est soumis aux forces de pesanteur qui tendent à effondrer l’étoile. L’énergie gravitationnelle libérée par la contraction des gaz chauffe l’étoile jusqu’à ce que les forces de pesanteur soient compensées par la pression cinétique des gaz [\(P=nkT\)] et du rayonnement [\(P=4\sigma T^4/(3c)\)]. Comme l’étoile rayonne, elle perd de l’énergie prélevée sur son potentiel gravitationnel et devrait donc continuer à se contracter lentement pour finir sous la forme d’un résidu dégénéré (c’est le destin des « naines brunes »). Toutefois, des réactions nucléaires exothermiques (fusion des éléments légers) prennent le relais et alimentent l’étoile en énergie (la chauffent) dès que la température centrale devient suffisante. En régime stationnaire, la puissance libérée par ces réactions nucléaires doit être égale à la luminosité de l’astre. Nous allons maintenant établir les équations pour l’équilibre hydrostatique (paragraphe 2.2) et energétique (paragraphe 2.3) de l’étoile.
Pour calculer les forces de pesanteur, il faut pouvoir relier la densité de masse \(\rho (r)\) dans l’étoile à la densité de particules (électrons et noyaux) \(n(r)\).
Une étoile est essentiellement constituée d’hydrogène (masse atomique \(m_\mathrm {H}=1.674\times 10^{-27}\)kg pour \(p_\mathrm {H}=2\) particules \(\equiv \) un proton et un électron), d’hélium (masse atomique \(m_\mathrm {He}\simeq 4m_\mathrm {H}\) pour \(p_\mathrm {He}=3\) particules \(\equiv \) un noyau \(\alpha \) et deux électrons), et d’autres éléments (appelés « métaux » en astrophysique) en petites quantités (\(m_\mathrm {*}\), \(p_\mathrm {*})\). On note \(X\) et \(Y\) les abondances en masse de l’hydrogène et de l’hélium, et \(Z=1-X-Y\) celle des métaux. La « métallicité » \(Z\) est un paramètre important2 qui conditionne la nucléosynthèse (cycle CNO) et le transfert radiatif dans l’étoile (voir paragraphe 2.3). On a donc :
\begin {equation} n=\rho \left (X\frac {p_\mathrm {H}}{m_\mathrm {H}}+Y\frac {p_\mathrm {He}}{m_\mathrm {He}}+Z\frac {p_\mathrm {*}}{m_\mathrm {*}}\right )=\frac {\rho }{m_\mathrm {H}}\left (2X+\frac {3}{4}Y+\frac {1}{2}Z\right )=\frac {\rho }{4m_\mathrm {H}}\left (6X+Y+2\right )\,, \end {equation}
où on a fixé3 \(p_\mathrm {*}/m_\mathrm {*}\approx 1/(2m_\mathrm {H})\). Soit encore
\begin {equation} \rho =n\mu m_\mathrm {H}\text { où }\mu =\frac {4}{6X+Y+2} \end {equation}
est la masse moyenne réduite des particules. C’est aussi (par définition de la mole) la masse moléculaire moyenne des particules en g/mol. On suppose en première approximation les abondances homogènes dans l’étoile, même si elles évoluent avec les réactions thermonucléaires, en particulier dans le coeur. Pour le Soleil4, \(X_\odot =0.7346\), \(Y_\odot =0.2485\), \(Z_\odot =0.0169\) et \(\mu _\odot =0.6\)g/mol. En négligeant \(Z\) devant \(X\) et \(Y\), la densité d’électrons dans l’étoile est en outre :
\begin {equation} n_\mathrm {e}\approx \rho \left (X\frac {1}{m_\mathrm {H}}+Y\frac {2}{m_\mathrm {He}}\right )\approx \frac {\rho }{m_\mathrm {H}}\left (X+\frac {1}{2}Y\right )\approx \frac {\rho }{2m_\mathrm {H}}\left (1+X\right )\,, \end {equation}
et celle des noyaux :
\begin {equation} n_\mathrm {n}\approx \rho \left (X\frac {1}{m_\mathrm {H}}+Y\frac {1}{m_\mathrm {He}}\right )\approx \frac {\rho }{m_\mathrm {H}}\left (X+\frac {1}{4}Y\right )\approx \frac {\rho }{4m_\mathrm {H}}\left (1+3X\right )\,. \end {equation}
A l’équilibre hydrostatique, la pression \(P(r)\) dans l’étoile doit vérifier la condition (1.121) :
\begin {equation} \frac {d}{dr}P(r)=\frac {d}{dr}[P_\mathrm {m}(r)+P_\mathrm {r}(r)]=-\rho (r)g(r)=-\rho (r)\frac {G{\cal M}(r)}{r^2}\,, \label {eq:eqhydro1} \end {equation}
où :
\begin {equation} {\cal M}(r)=4\pi \int _0^r dr^\prime \,r^{\prime 2}\rho (r^\prime ) \label {eq:eqhydro2} \end {equation}
est la masse totale enclose dans la sphère de rayon \(r\), et :
\begin {align} &P_\mathrm {m}(r)=\frac {\rho (r)}{\mu }N_\mathrm {A}kT(r)=\frac {\rho (r)}{\mu }{\cal R}T(r) \label {eq:eqhydro3} \\ &P_\mathrm {r}(r)=\frac {1}{3}aT(r)^4=\frac {4\sigma }{3c}T(r)^4 \label {eq:eqhydro4} \end {align}
sont respectivement la pression de la matière et du rayonnement à la température \(T(r)\) (avec \(N_\mathrm {A}=6.022\times 10^{23}\) le nombre d’Avogadro, \({\cal R}=N_\mathrm {A}k=8.314\)J/K/mol la constante des gaz parfaits, et \(\mu =0.6\)g/mol pour le Soleil).
L’équation \eqref{eq:eqhydro1}–\eqref{eq:eqhydro4} couple la densité de masse \(\rho (r)\) à la température \(T(r)\) dans l’étoile (laquelle donne la pression \(P(r)\)). Il manque donc une deuxième équation pour compléter ce système, dérivée du bilan énergétique de l’étoile. Néanmoins, nous pouvons déjà utiliser \eqref{eq:eqhydro1}–\eqref{eq:eqhydro4} pour estimer les températures et pressions régnant dans des étoiles comme le Soleil.
A cet effet, nous allons supposer en toute première approximation que le Soleil est une sphère homogène de rayon \(R_\odot =696\,340\)km et de masse \(M_\odot =2\times 10^{30}\)kg (donc de densité \(\rho _\odot =3M_\odot /(4\pi R_\odot ^3)=1414\)kg/m\(^3\)) [1]. Par conséquent,
\begin {equation} {\cal M}(r\le R)=M_\odot \left (\frac {r}{R_\odot }\right )^3\text {\ et }{\cal M}(r\ge R)=M_\odot \,. \end {equation}
A l’intérieur du Soleil,
\begin {equation} \frac {d}{dr}P(r)=-\rho _\odot \frac {G{\cal M}(r)}{r^2}=-\frac {3GM_\odot ^2}{4\pi R_\odot ^6}r\,, \end {equation}
si bien que :
\begin {equation} P(0)-P(R)=\frac {3GM_\odot ^2}{8\pi R_\odot ^4}\,. \end {equation}
En négligeant \(P(R)\) devant \(P(0)\), la pression centrale vaut donc :
\begin {equation} P(0)=\frac {3GM_\odot ^2}{8\pi R_\odot ^4}\approx 135\,000\,\text {GPa}\,, \label {eq:P0} \end {equation}
soit \(1.34\) milliards d’atmosphères. On estime ensuite la température centrale \(T(0)\) en supposant \(P(0)\approx P_\mathrm {m}(0)\) :
\begin {equation} T(0)=\frac {\mu _\odot P(0)}{\rho _\odot {\cal R}}=\frac {\mu _\odot }{\cal R}\frac {GM_\odot }{2R_\odot }\approx 7\times 10^6\,\text {K}\,. \label {eq:T0} \end {equation}
Cette valeur – quoi que du bon ordre de grandeur – est sous-estimée car la densité, et donc la pression et la température augmentent au coeur du Soleil (en réalité \(T(0)\approx 15\times 10^6\)K).
Les réactions thermonucléaires au coeur de l’étoile libèrent de l’énergie qui est transférée vers sa surface. On appelle \({\cal L}(r)\) la quantité d’énergie traversant chaque unité de temps une coquille de rayon \(r\) (débit d’énergie ou puissance). On note également \(\varepsilon _\mathrm {n}(\vec {r})\equiv \varepsilon _\mathrm {n}(r)\) la quantité d’énergie thermonucléaire produite au point \(\vec {r}\) par unité de temps et de masse (puissance massique). En régime stationnaire, la conservation de l’énergie implique :
\begin {equation} {\cal L}(r+dr)-{\cal L}(r)=4\pi r^2 dr\rho (r)\varepsilon _\mathrm {n}(r)\,, \end {equation}
soit :
\begin {equation} \frac {d}{dr}{\cal L}(r)=4\pi r^2\rho (r)\varepsilon _\mathrm {n}(r)\,, \label {eq:dLdr} \end {equation}
qui s’intègre immédiatement :
\begin {equation} {\cal L}(r)= 4\pi \int _0^r dr^\prime r^{\prime 2}\rho (r^\prime )\varepsilon _\mathrm {n}(r^\prime )\,. \label {eq:Lr} \end {equation}
C’est ce débit d’énergie qui chauffe l’étoile et entretient sa luminosité. On doit par conséquent avoir :
\begin {equation} {\cal L}(r\to \infty )=L \end {equation}
où \(L\) est la luminosité de l’étoile [Eq. (1.79)] ; autrement dit :
\begin {equation} L=4\pi \int _0^\infty dr\, r^2\rho (r)\varepsilon _\mathrm {n}(r)\approx 4\pi \int _0^Rdr\, r^2\rho (r)\varepsilon _\mathrm {n}(r)\,, \end {equation}
est la puissance totale produite par les réactions thermonucléaires (avec \(R\) le rayon de l’étoile, à definir). Nous allons maintenant discuter quels sont les mécanismes qui permettent de transférer l’énergie dans l’étoile et de maintenir l’équilibre thermodynamique local : la conduction (échange d’énergie cinétique au cours des collisions entre particules), le transfert radiatif (par les photons), et la convection (transport de matière à grande échelle).
Tout ou partie de cette énergie peut-être transférée par échange de quantité de mouvement entre (quasi-)particules (conduction thermique) ; les étoiles étant essentiellement gazeuses, et dans l’ensemble relativement peu denses (en dehors du coeur), la conduction thermique y est néanmoins peu efficace5.
L’énergie peut-être transportée par les photons, lesquels vont être diffusés et absorbés par les gaz, permettant ainsi la thermalisation du couple lumière/matière ; pour décrire ce phénomène, on introduit le coefficient d’extinction (ou opacité) \(\kappa (\nu )\) tel que la luminance énergétique spectrale d’un faisceau de lumière traversant une épaisseur \(dl\) de matière soit atténuée de :
\begin {equation} dL(\Theta ,\Phi ,\nu ,\vec {r})=-\rho (\vec {r})\kappa (\nu ,\vec {r})L(\Theta ,\Phi ,\nu ,\vec {r})dl\,, \end {equation}
avec \((\Theta ,\Phi )\) la direction d’émission et \(\nu \) la fréquence des photons (loi de Beer-Lambert). Si le libre parcours moyen \(\ell (\nu )=[\rho (\vec {r})\kappa (\nu ,\vec {r})]^{-1}\) des photons est constant,
\begin {equation} L(\Theta ,\Phi ,\nu ,\vec {r})\propto e^{-l/\ell (\nu )}\,. \end {equation}
En toute généralité, il convient d’ajouter un terme « source » \(j(\nu ,\vec {r})\) supposé isotrope :
\begin {equation} dL(\Theta ,\Phi ,\nu ,\vec {r})=\rho (\vec {r})[j(\nu ,\vec {r}) -\kappa (\nu ,\vec {r})L(\Theta ,\Phi ,\nu ,\vec {r})]dl\,. \end {equation}
Ce terme source décrit notamment l’émission spontanée dans le milieu6. A l’équilibre thermodynamique à la température \(T\),
\begin {equation} L(\Theta ,\Phi ,\nu ,\vec {r})=L_\mathrm {eq}(\nu ,T)=\frac {2h\nu ^3}{c^2}\frac {1}{e^{\beta h\nu }-1} \end {equation}
est indépendante de la position (loi de Planck) ; \(\kappa (\nu ,\vec {r})\) et \(j(\nu ,\vec {r})\) doivent donc être liées par la relation :
\begin {equation} dL(\Theta ,\Phi ,\nu ,\vec {r})=0\Rightarrow \frac {j_\mathrm {eq}(\nu ,\vec {r})}{\kappa _\mathrm {eq}(\nu ,\vec {r})}=L_\mathrm {eq}(\nu ,T)=\frac {2h\nu ^3}{c^2}\frac {1}{e^{\beta h\nu }-1}\,. \label {eq:bilandetaille} \end {equation}
Dans le Soleil, \(\ell (\nu )\) varie de 0.01 à 1cm en dehors de la photosphère (la surface visible de l’étoile, où les gaz deviennent transparents). Les étoiles sont donc des milieux relativement opaques.

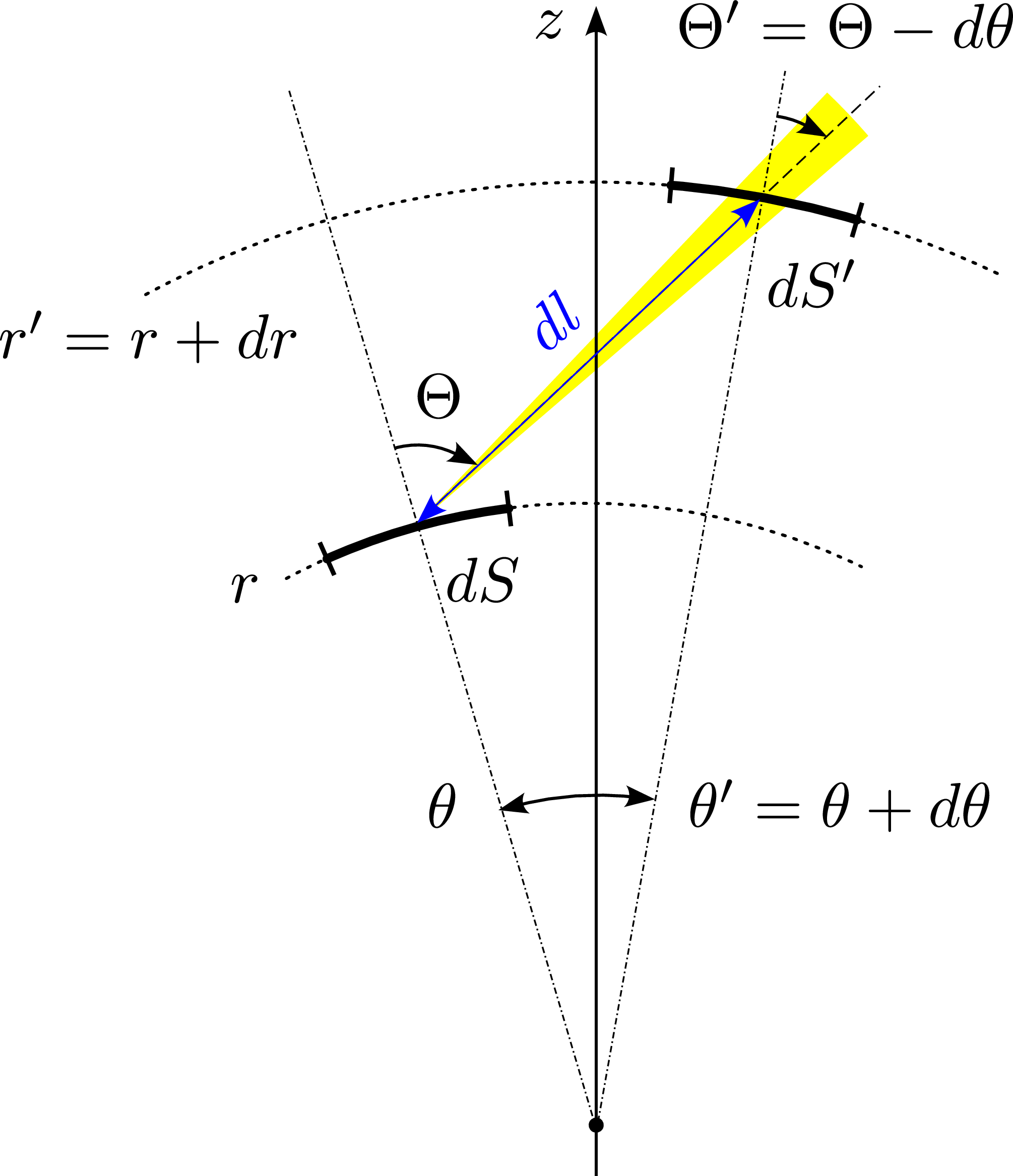
Nous allons maintenant établir l’équation de transfert radiatif en symétrie et coordonnées sphériques. En mesurant l’angle d’émission \(\Theta \) par rapport au rayon vecteur \(\vec {r}\) (voir Fig. 2.1), la symétrie de révolution autour de cet axe impose \(L(\Theta ,\Phi ,\nu ,\vec {r})\equiv L(\Theta ,\nu ,r)\). Imaginons un élément de surface \(dS\) en \((r,\theta ,\varphi )\), émettant dans la direction \((\Theta ,\Phi )\) vers un autre élément de surface \(dS^\prime \) interceptant le faisceau en \((r^\prime =r+dr,\theta ^\prime =\theta +d\theta ,\varphi ^\prime =\varphi +d\varphi )\) avec des angles \((\Theta ^\prime =\Theta +d\Theta =\Theta -d\theta ,\Phi ^\prime =\Phi )\). La loi de Beer-Lambert pour la luminance énergétique spectrale s’écrit :
\begin {equation} L(\Theta +d\Theta ,\nu ,r+dr)-L(\Theta ,\nu ,r)=\rho (r)[j(\nu ,r)-\kappa (\nu ,r)L(\Theta ,\nu ,r)]dl\,. \end {equation}
Soit (en laissant les variables implicites par souci de lisibilité, cf. notations du paragraphe 1.3) :
\begin {equation} \frac {\partial L_{\Omega ,\nu }}{\partial r}dr+\frac {\partial L_{\Omega ,\nu }}{\partial \Theta }d\Theta =\rho [j_\nu -\kappa _\nu L_{\Omega ,\nu }]dl\,. \end {equation}
Ensuite,
\begin {align} &dr=dl\cos \Theta \\ &rd\theta =-rd\Theta =dl\sin \Theta \,, \end {align}
si bien que :
\begin {equation} \frac {\partial L_{\Omega ,\nu }}{\partial r}\cos \Theta -\frac {1}{r}\frac {\partial L_{\Omega ,\nu }}{\partial \Theta }\sin \Theta =\rho [j_\nu -\kappa _\nu L_{\Omega ,\nu }]\,. \label {eq:eqtradint1} \end {equation}
On peut tout d’abord intégrer cette équation sur la fréquence \(\nu \) ; en supposant dans un premier temps \(\kappa _\nu \equiv \kappa \) constant,
\begin {equation} \frac {\partial L_\Omega }{\partial r}\cos \Theta -\frac {1}{r}\frac {\partial L_\Omega }{\partial \Theta }\sin \Theta =\rho [j-\kappa L_\Omega ]\,. \end {equation}
On multiplie ensuite le tout par \(\cos \Theta \) et on intègre sur l’angle solide \(\Omega \). Comme \(L_\Omega \) a la symétrie de révolution, on peut utiliser les relations (1.86)–(1.88) :
\begin {align} \int _{0}^{2\pi }d\Phi &\int _0^\pi d\Theta \,\sin \Theta \cos ^2\Theta \,L_\Omega =\hat {\mu }_2(L_\Omega )=cP_\mathrm {r}\,, \\ \int _{0}^{2\pi }d\Phi &\int _0^\pi d\Theta \,\sin ^2\Theta \cos \Theta \,\frac {\partial L_\Omega }{\partial \Theta } \nonumber \\ &=-\int _{0}^{2\pi }d\Phi \int _0^\pi d\Theta \,(3\cos ^2\Theta \sin \Theta -\sin \Theta )\,L_\Omega \text {\ (par parties)} \nonumber \\ &=-3\hat {\mu }_2(L_\Omega )+\hat {\mu }_0(L_\Omega )=-3cP_\mathrm {r}+c\eta _\mathrm {r}\,, \\ \int _{0}^{2\pi }d\Phi &\int _0^\pi d\Theta \,\sin \Theta \cos \Theta \, L_\Omega =\hat {\mu }_1(L_\Omega )=F_\mathrm {r}\,, \\ \int _{0}^{2\pi }d\Phi &\int _0^\pi d\Theta \,\sin \Theta \cos \Theta \,j=0\text {\ ($j$ isotrope).} \end {align}
Par conséquent,
\begin {equation} \frac {d}{dr}P_\mathrm {r}(r)+\frac {1}{r}[3P_\mathrm {r}(r)-\eta _\mathrm {r}(r)]=-\frac {1}{c}\rho (r)\kappa (r)F_\mathrm {r}(r)\,. \label {eq:eqtradint2} \end {equation}
Cette équation ne présuppose pas l’équilibre thermodynamique local et s’applique donc quelle que soit la fonction de distribution des photons. Si on admet maintenant que les photons sont localement à l’équilibre thermodynamique à la température \(T(r)\), alors \(P_\mathrm {r}(r)=\eta _\mathrm {r}(r)/3=4\sigma T(r)^4/(3c)\) et
\begin {equation} \frac {d}{dr}\eta _\mathrm {r}(r)=-\frac {3}{c}\rho (r)\kappa (r)F_\mathrm {r}(r)\,, \label {eq:detadr} \end {equation}
soit encore :
\begin {equation} \frac {d}{dr}T(r)=-\frac {3}{16\sigma }\frac {\rho (r)\kappa (r)}{T(r)^3}F_\mathrm {r}(r)\,. \end {equation}
Enfin, si l’énergie est exclusivement transférée par le rayonnement, la densité de flux radiatif est \(F_\mathrm {r}(r)={\cal L}(r)/(4\pi r^2)\), de sorte que :
\begin {equation} \frac {d}{dr}T(r)=-\frac {3}{16\sigma }\frac {\rho (r)\kappa (r)}{T(r)^3}\frac {{\cal L}(r)}{4\pi r^2}=-\frac {3}{16\sigma }\frac {1}{\ell (r)T(r)^3}\frac {{\cal L}(r)}{4\pi r^2}\,. \end {equation}
Cette équation lie le gradient de température7 au débit d’énergie et au libre parcours moyen des photons dans l’étoile. Lorsque la matière absorbe la lumière, elle gagne de l’énergie et se réchauffe au dépend du bain de photons qui perd de l’énergie [Eq. \eqref{eq:detadr}] et se refroidit. Comme matière et rayonnement restent partout à l’équilibre, le gradient de température est négatif et la longueur d’onde moyenne des photons augmente progressivement. On peut alternativement introduire la conductivité thermique \(\lambda _\mathrm {th}\) du milieu telle que :
\begin {equation} F_\mathrm {r}=-\lambda _\mathrm {th}\frac {dT}{dr}\ \Rightarrow \ \lambda _\mathrm {th}=\frac {16}{3}\sigma \ell T^3\,. \end {equation}
La conductivité thermique est d’autant plus importante, et la température d’autant plus homogène que le libre parcours moyen des photons est grand (donc que ceux-ci transfèrent l’énergie sur de longues distances). Au fur et à mesure que la température diminue, les photons ont de moins en moins d’énergie [\(E=h\nu \propto kT\)] et de modes pour les porter [\(\rho (\nu )\propto \nu ^2\propto (kT)^2\)], de sorte que \(dT/dr\propto T^{-3}\) augmente pour un même débit d’énergie absorbée (il faut « vider » les modes de photons sur une gamme d’énergie croissante). Ce fort gradient de température peut finir par déstabiliser l’équilibre hydrostatique et déclencher des mouvements de convection (voir ci-dessous).
En pratique, \(\kappa _\nu \) est très dépendent de la fréquence des photons. Il aggrège les contributions de différents mécanismes : absorption entre états liés d’atomes neutres ou incomplètement ionisés (transitions lié \(\rightarrow \) lié), ionisation de ces mêmes atomes (transitions lié \(\rightarrow \) libre), collisions électrons-ions inélastiques (Bremsstrahlung inverse, transitions libre \(\rightarrow \) libre) et diffusion Compton des photons... On peut définir un \(\kappa \) moyen ou effectif à partir de la décomposition spectrale \eqref{eq:eqtradint1} à l’équilibre thermodynamique local. En multipliant d’abord par \(\cos \Theta \), puis en intégrant sur l’angle solide, et en négligeant les termes source et \(\partial L_\Omega /\partial \Theta \) qu’on sait ne pas contribuer, il vient :
\begin {equation} \frac {4\pi }{3}\frac {d}{dr}L_{\Omega ,\nu }(\nu ,T)=-\rho \kappa (\nu )F_\mathrm {r}(\nu )\,, \end {equation}
où \(F_\mathrm {r}(\nu )\) est le flux radiatif par unité de fréquence. Soit :
\begin {equation} F_\mathrm {r}(\nu )=-\frac {4\pi }{3\rho \kappa (\nu )}\frac {d}{dr}L_{\Omega ,\nu }(\nu ,T)=-\frac {4\pi }{3\rho \kappa (\nu )}\frac {\partial }{\partial T}L_{\Omega ,\nu }(\nu ,T)\frac {dT}{dr}\,. \end {equation}
En intégrant enfin sur la fréquence,
\begin {equation} F_\mathrm {r}=\int _0^\infty d\nu \,F_\mathrm {r}(\nu )=-\frac {4\pi }{3\rho }\frac {dT}{dr}\int _0^\infty d\nu \,\frac {1}{\kappa (\nu )}\frac {\partial }{\partial T}L_{\Omega ,\nu }(\nu ,T)\,, \end {equation}
que l’on cherche à identifier avec \eqref{eq:eqtradint2} :
\begin {align} F_\mathrm {r}&=-\frac {c}{\rho \kappa }\frac {d}{dr}P_\mathrm {r}=-\frac {4\pi }{3\rho \kappa }\int _0^\infty d\nu \,\frac {d}{dr}L_{\Omega ,\nu }(\nu ,T) \nonumber \\ &=-\frac {4\pi }{3\rho }\frac {dT}{dr}\int _0^\infty d\nu \,\frac {1}{\kappa }\frac {d}{dT}L_{\Omega ,\nu }(\nu ,T)\,. \end {align}
On peut à cet effet introduire la « moyenne de Rosseland » \(\kappa (T)\) définie par la relation :
\begin {equation} \frac {1}{\kappa (T)}=\left [\int _0^\infty d\nu \,\frac {\partial }{\partial T}L_{\Omega ,\nu }(\nu ,T)\right ]^{-1}\int _0^\infty d\nu \,\frac {1}{\kappa (\nu )}\frac {\partial }{\partial T}L_{\Omega ,\nu }(\nu ,T)\,, \end {equation}
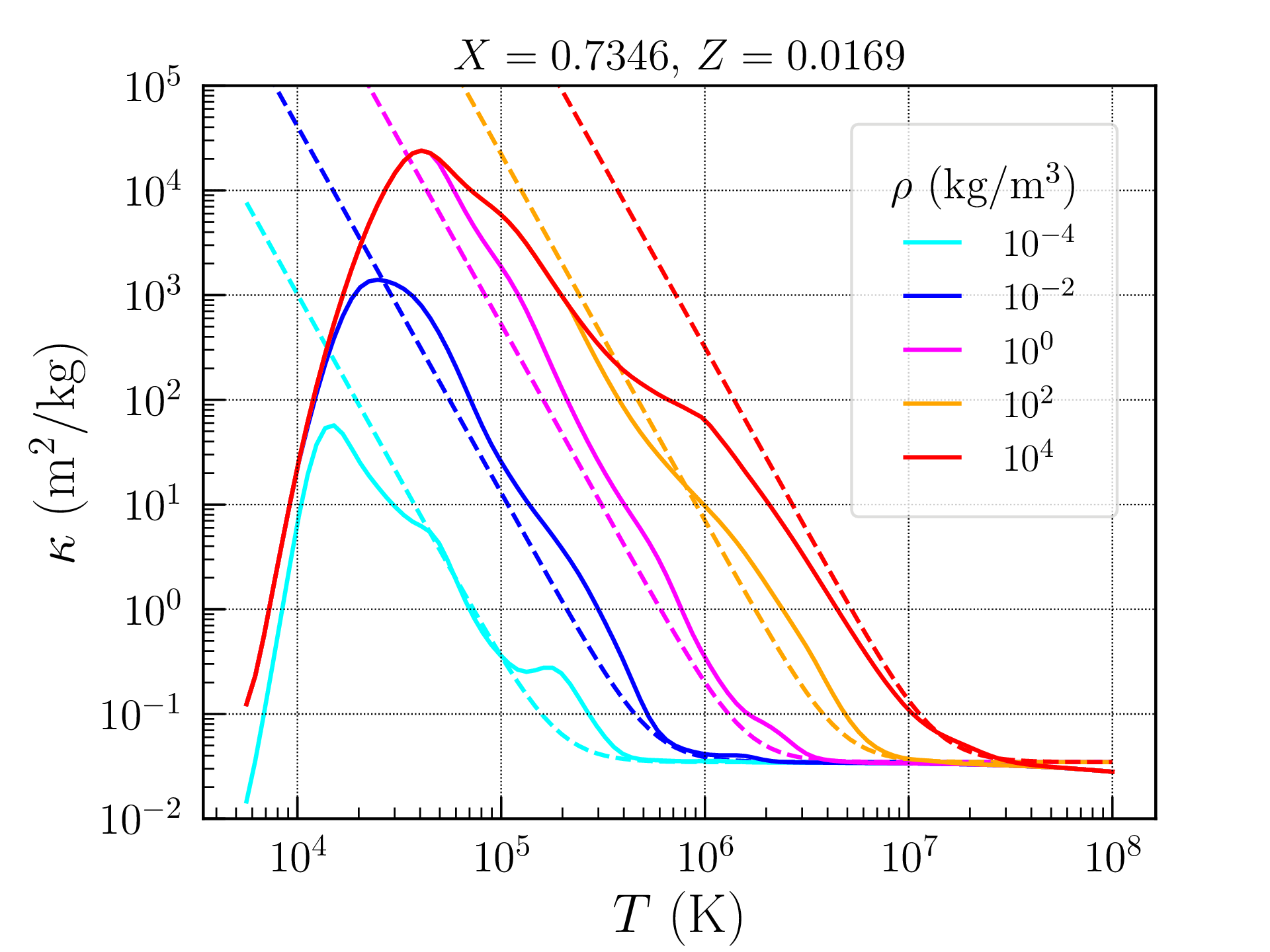
avec \(L_{\Omega ,\nu }(\nu ,T)\) donné par la loi de Planck (1.73). Ce \(\kappa (T)\) moyen présente typiquement un pic vers \(T\approx 50\,000\)K (voir Figure 2.2). En effet, à plus basse température, les atomes ne sont plus – ou seulement partiellement – ionisés. L’absorption libre \(\rightarrow \) libre (collisions électrons-ions) diminue donc, tandis que l’absorption lié \(\rightarrow \) libre devient de plus en plus difficile. La température est, en particulier, rapidement insuffisante pour ioniser l’hydrogène (mais pas son ion H\(^-\) qui peut dominer l’opacité malgré sa faible abondance). L’absorption lié \(\rightarrow \) lié entre niveaux atomiques ne se produit quant à elle qu’à des fréquences de résonance bien particulières. Le milieu se fait ainsi de plus en plus transparent. Dans ce régime, le transfert d’énergie se fait cependant plutôt par convection (voir paragraphe 2.3.3) que par radiation. A plus haute température, presque tous les atomes sont à l’inverse complètement ionisés ; il y a donc de moins en moins de transitions lié \(\rightarrow \) lié ou lié \(\rightarrow \) libre, tandis que le Bremsstrahlung inverse devient inefficace à haute énergie. Les références [6-8] proposent les comportements haute température suivants pour l’opacité (lois de Kramers) :
Pour les transitions lié \(\rightarrow \) libre,
Pour les transitions libre \(\rightarrow \) libre,
Pour la diffusion Compton,
Dans ces expressions, \(\rho \) est exprimée en kg/m\(^3\) et \(T\) en Kelvins. \(g_\mathrm {bf}\) et \(g_\mathrm {ff}\) sont des « facteurs de Gaunt » proches de 1, et \(t\) est un « facteur de guillotine » destiné à corriger la surestimation du nombre d’électrons liés à haute température (\(t=1-100\), typiquement \(t\simeq 10\)). On pourra faire l’approximation suivante :
\begin {equation} t\approx 0.71\left [\rho (1+X)\right ]^{0.2}\,. \label {eq:tbf} \end {equation}
Le libre parcours moyen \(\ell \equiv (\rho \kappa )^{-1}\) est toujours proportionnel à la densité d’électrons \(n_\mathrm {e}\propto \rho (1+X)\). L’absorption lié \(\rightarrow \) libre est en effet proportionnelle à la densité de métaux \(\rho Z\) car les atomes conservent d’autant plus d’électrons liés qu’ils sont lourds, et à la vitesse \(\propto n_\mathrm {e}\) à laquelle les niveaux ionisés sont repeuplés. L’absorption libre \(\rightarrow \) libre est proportionnelle à la densité d’électrons \(n_\mathrm {e}\) et à la densité totale \(\rho \) (s’agissant de collisions inélastiques électrons-ions). L’absorption libre \(\rightarrow \) libre a donc tendance à dominer dans les étoiles de population II très pauvres en métaux, alors que l’absorption lié \(\rightarrow \) libre prend le pas dans les étoiles de population I, plus riches en éléments lourds. La diffusion Compton est simplement proportionnelle à la densité d’électrons \(n_\mathrm {e}\) pouvant interagir avec un photon. Dans sa limite élastique (diffusion Thomson), l’opacité est indépendente de la température.
L’opacité moyenne de Rosseland peut être calculée et tabulée à partir d’une solution numérique des équations décrivant les interactions lumière-matière dans l’étoile et les spectres d’absorption des éléments constituants dans leurs états d’ionisation possibles. Des tables de \(\kappa (\rho ,T)\) pour différentes compositions stellaires sont ainsi disponibles dans la littérature et mises à disposition de la communauté scientifique, telles que celles du projet OPAL [9]. Les opacités OPAL pour la composition solaire sont comparées aux lois de Kramers \eqref{eq:kappabf}–\eqref{eq:tbf} sur la figure 2.2 (voir les codes opacity.py et star.py). Les lois de Kramers reproduisent raisonnablement l’opacité pour des températures \(T>100\,000\)K.
Les équations de transfert radiatif ont été établies en régime stationnaire et ne disent donc rien de l’échelle de temps nécessaire pour atteindre ce régime ou y revenir après une perturbation. Ce temps caractéristique est par nature comparable à celui que met un photon émis au coeur de l’étoile pour atteindre sa surface. On peut donner une estimation, certes grossière, mais instructive de la durée de ce transit avec un modèle diffusif simple. On suppose à cet effet que les photons effectuent des vols libres dans l’étoile entrecoupés de collisions (diffusion ou absorption/réémission) desquelles ils ressortent dans une direction aléatoire. La position d’un photon émis du centre à \(t=0\) est, au bout de \(N\) collisions :
\begin {equation} \vec {R}_N=\sum _{i=1}^N \vec {r}_i\,, \end {equation}
où \(\vec {r}_i\) est le chemin parcouru entre les collisions \(i-1\) et \(i\). Par conséquent, on a en moyenne
\begin {equation} \langle \vec {R}_N^2 \rangle =\sum _{i=1}^N\sum _{j=1}^N \langle \vec {r}_i\cdot \vec {r}_j\rangle =\sum _{i=1}^N \langle \vec {r}_i^2\rangle \,, \end {equation}
car \(\langle \vec {r}_i\rangle =\vec {0}\) sur chaque chemin, lesquels sont par ailleurs indépendants. En assimilant \(\langle \vec {r}_i^2\rangle \approx \ell ^2\) au libre parcours moyen carré,
\begin {equation} \langle \vec {R}_N^2\rangle \approx N\ell ^2\,. \end {equation}
Enfin, le nombre de collisions subies au temps \(t\) est \(N\approx t/\Delta t\), où \(\Delta t=\ell /c\) est le temps moyen séparant deux d’entre elles, si bien que :
\begin {equation} \langle \vec {R}^2(t)\rangle \approx tc\ell \,. \end {equation}
Le photon se trouve donc à une distance moyenne du centre :
\begin {equation} \overline {R}(t)=\sqrt {\langle \vec {R}^2(t)\rangle }\approx \sqrt {tc\ell }\,, \end {equation}
et atteint la surface en un temps caractéristique de diffusion :
\begin {equation} t_\mathrm {diff}=\frac {R^2}{c\ell }\,, \end {equation}
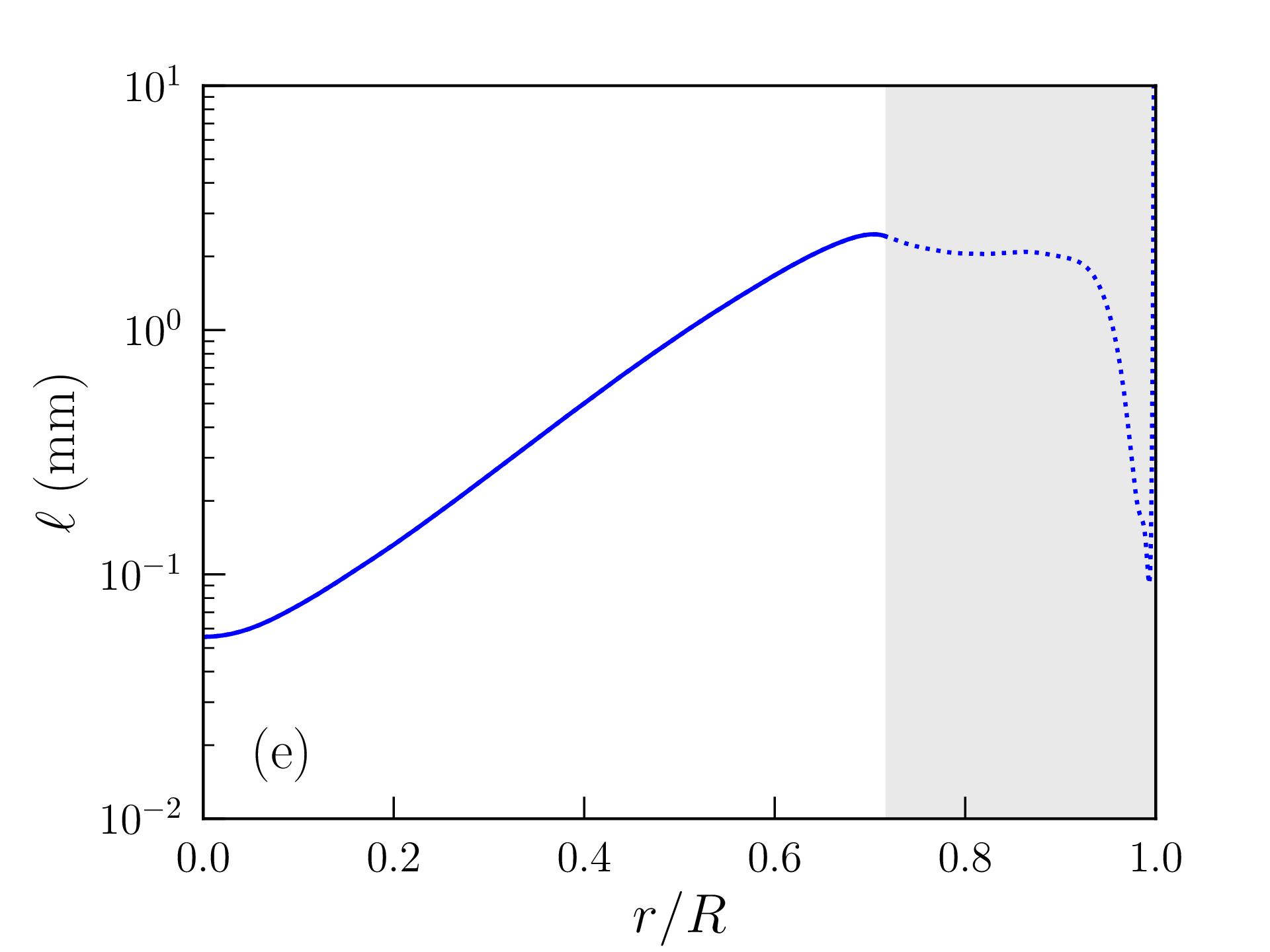
où \(R\) est le rayon de l’étoile. Pour le Soleil, \(R_\odot =696\,340\)km, et en prenant \(\ell \approx 1\)mm, \(t_\mathrm {diff}\approx 50\,000\)ans. Le transfert radiatif au sein d’une étoile est donc particulièrement lent.
Lorsque le milieu se fait plus opaque ou plus froid, le gradient de température radiatif augmente, ce qui finit par déstabiliser l’équilibre hydrostatique de la matière qui s’anime de mouvements de convection : les gaz chauds remontent vers la surface où ils se refroidissent par détente et rayonnement avant de replonger vers les profondeurs. Le transfert de chaleur est alors essentiellement assuré par ces « cellules » de convection. La description détaillée de telles cellules relève en principe d’une approche hydrodynamique. Nous allons ici établir un modèle minimal pour le régime convectif basé sur des considérations thermodynamiques. Pour commencer, nous allons rappeler les conditions de détente adiabatique d’un gaz.
Dans un gaz parfait classique, l’énergie interne \(E\) est proportionnelle à \(NT\) (en vertu du théorème d’équipartition de l’énergie8), de même que l’enthalpie \(H=E+PV\) (car \(PV=NkT\)). Nous pouvons donc introduire les capacités thermiques isochore \(c_\mathrm {v}\) et isobare \(c_\mathrm {p}\) par particule de gaz telles que :
\begin {align} E&=Nc_\mathrm {v}T \\ H&=Nc_\mathrm {p}T \,. \end {align}
Ainsi, lors d’une transformation adiabatique où seules les forces de pression fournissent un travail \(dW=-PdV\),
\begin {align} dE&=Nc_\mathrm {v}dT=dW=-PdV \\ dH&=Nc_\mathrm {p}dT=dE+PdV+VdP=VdP \,. \end {align}
On conclut du ratio de ces deux quantités que :
\begin {equation} \gamma \frac {dV}{V}+\frac {dP}{P}=d\log \left (PV^\gamma \right )=0\,, \end {equation}
où \(\gamma =c_\mathrm {p}/c_\mathrm {v}\) est le coefficient adiabatique du gaz. En introduisant la relation \(PV=NkT\), il vient indifféremment :
\begin {equation} d(PV^\gamma )=d(TV^{\gamma -1})=d(T^\gamma P^{1-\gamma })=0\,. \label {eq:Laplace2} \end {equation}
Dans un gaz parfait « monoatomique » (sans degrés de liberté internes9), \(c_\mathrm {v}=\frac {3}{2}k\) par particule, tandis que \(c_\mathrm {p}=c_\mathrm {v}+k=\frac {5}{2}k\) par particule, si bien que \(\gamma =5/3\). On retrouve là la loi de Laplace (1.38).
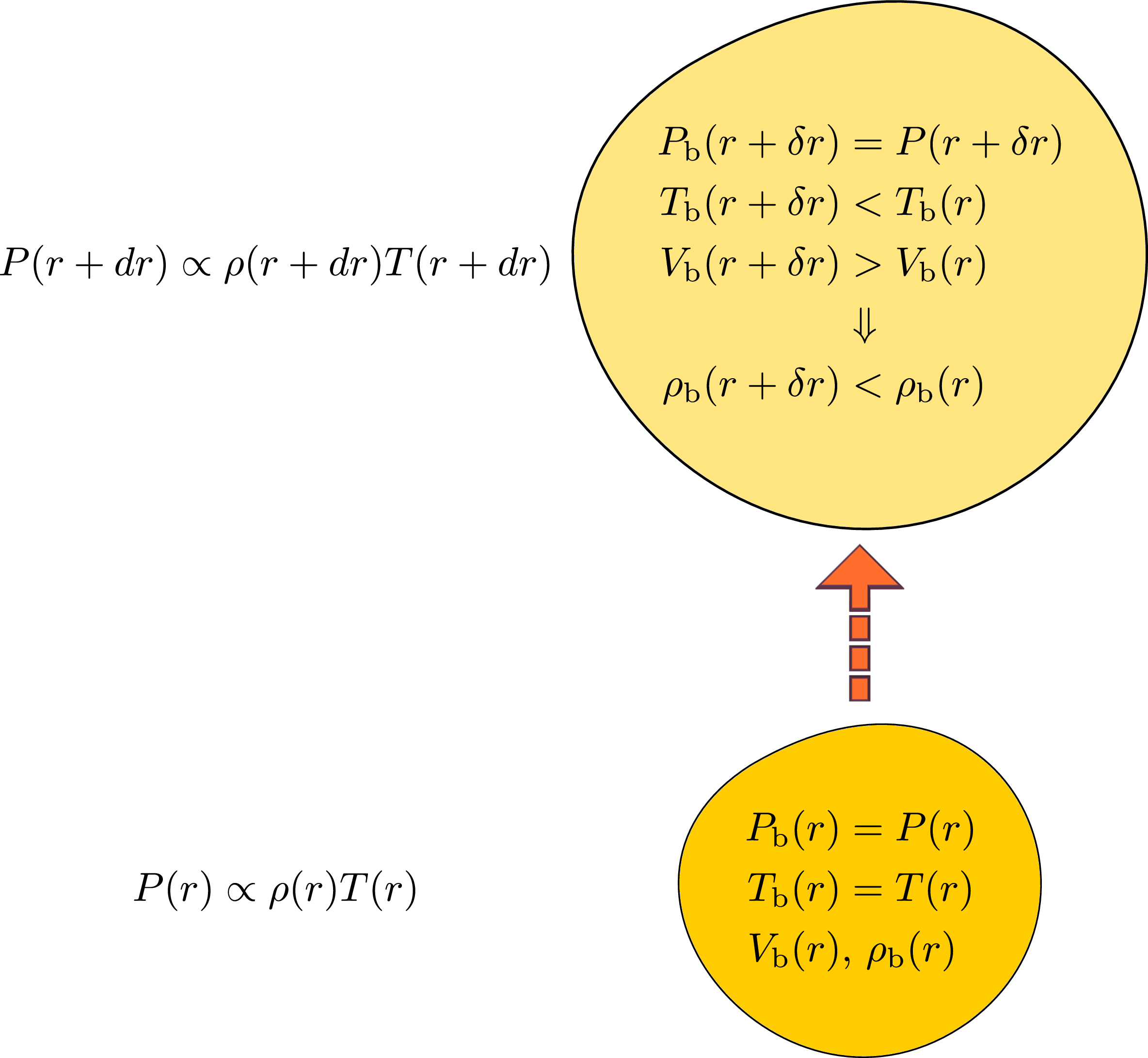
La convection se manifeste par la rupture de l’équilibre hydrostatique et la mise en mouvement de grandes quantités de gaz qui font circuler la matière et transférent l’énergie dans l’étoile. Imaginons une « bulle » de gaz à la position radiale \(r\), contenant \(N_\mathrm {b}\) particules dans un volume \(V_\mathrm {b}\), initialement en équilibre hydrostatique et thermique avec son milieu, mais déstabilisée par une « poussée vers le haut » d’origine quelconque (Fig. 2.3). A quelle condition cette bulle de gaz peut-elle continuer à s’élever, portée par le gradient de pression dans le milieu10, initiant ainsi le mouvement de convection?
Supposons dans un premier temps que la bulle reste en équilibre avec la pression \(P(r)\) du milieu et se détende de façon adiabatique en remontant le gradient de pression (donc sans échanger de chaleur avec son environnement). On a alors dans la bulle qui s’est élevée de \(\delta r\) :
\begin {equation} d(PV_\mathrm {b}^\gamma )=0\Rightarrow P(r)V_\mathrm {b}(r)^\gamma = P(r+\delta r)V_\mathrm {b}(r+\delta r)^\gamma \Rightarrow \frac {P(r+\delta r)}{P(r)}=\left (\frac {\rho _\mathrm {b}(r+\delta r)}{\rho _\mathrm {b}(r)}\right )^\gamma \,, \end {equation}
où \(\rho _\mathrm {b}(r)\) est la densité de masse dans la bulle (avec, à l’origine de la détente \(\rho _\mathrm {b}(r)=\rho (r)\), la densité de masse dans le milieu). Soit :
\begin {equation} \rho _\mathrm {b}(r+\delta r)=\rho (r)\left (1+\frac {1}{P(r)}\frac {d}{dr}P(r)\delta r\right )^\frac {1}{\gamma }\approx \rho (r)\left (1+\frac {1}{\gamma }\frac {1}{P(r)}\frac {d}{dr}P(r)\delta r\right )\,. \end {equation}
La bulle continue à s’élever naturellement (portée par la poussée d’Archimède, cf. chapitre 1) si sa densité \(\rho _\mathrm {b}(r+\delta r)\) est inférieure à la densité \(\rho (r+\delta r)\) du milieu :
\begin {align} \rho _\mathrm {b}(r+\delta r)<\rho (r+\delta r)&\Rightarrow \frac {1}{\gamma }\frac {1}{P(r)}\frac {d}{dr}P(r)<\frac {1}{\rho (r)}\frac {d}{dr}\rho (r) \nonumber \\ &\Rightarrow \frac {1}{\gamma }\frac {d}{dr}\log P(r)<\frac {d}{dr}\log \rho (r)\,. \end {align}
Comme \(P(r)=\rho (r){\cal R}T(r)/\mu \) dans le milieu, cette condition s’écrit équivalemment :
\begin {align} \frac {1}{\gamma }\frac {d}{dr}\log P(r)&<\frac {d}{dr}\log P(r)-\frac {d}{dr}\log T(r) \nonumber \\ \Rightarrow \frac {d}{dr}\log T(r)&<\left (1-\frac {1}{\gamma }\right )\frac {d}{dr}\log P(r) \nonumber \\ \Rightarrow \frac {d}{dr}T(r)&<T^\prime _c(r)\,. \end {align}
où \(T^\prime _c(r)\) est le « gradient thermique adiabatique » :
\begin {equation} T^\prime _c(r)=\left (1-\frac {1}{\gamma }\right )\frac {T(r)}{P(r)}\frac {d}{dr}P(r)\,. \label {eq:Tpc} \end {equation}
Puisque la pression et la température décroissent normalement avec \(r\), la convection démarre lorsque la valeur absolue du gradient de température devient trop grande au regard de celle du gradient de pression. En introduisant à nouveau la relation \(P(r)=\rho (r){\cal R}T(r)/\mu \) et la condition d’équilibre hydrostatique (1.121) dans \eqref{eq:Tpc}, il vient :
\begin {equation} T^\prime _c(r)=-\frac {\mu }{{\cal R}}\left (1-\frac {1}{\gamma }\right )g(r)\,. \end {equation}
On obtient finalement le critère de convection de Schwarzschild en écrivant \(1-1/\gamma =(c_\mathrm {p}-c_\mathrm {v})/c_\mathrm {p}=k/c_\mathrm {p}\) et en introduisant la capacité calorifique isobare par unité de masse \(C_\mathrm {p}=N_\mathrm {A}c_\mathrm {p}/\mu \) :
\begin {equation} \text {La convection démarre dès que }\frac {d}{dr}T(r)<T^\prime _c(r)=-\frac {g(r)}{C_\mathrm {p}}\,. \end {equation}
Nous pouvons également établir la variation de la température \(T_\mathrm {b}(r)\) de la bulle lors de sa détente adiabatique. Comme \(d(T_\mathrm {b}^\gamma P^{1-\gamma })=0\),
\begin {equation} \frac {d}{dr}T_\mathrm {b}(r)=\left (1-\frac {1}{\gamma }\right )\frac {T_\mathrm {b}(r)}{P(r)}\frac {d}{dr}P(r)=\frac {T_\mathrm {b}(r)}{T(r)}T^\prime _c(r)\,. \end {equation}
Puisque \(T^\prime _c(r)<0\), le gaz se refroidit (comme attendu) en se détendant. On a notamment à l’origine de la détente :
\begin {equation} \frac {d}{dr}T_\mathrm {b}(r)=T^\prime _c(r)\,. \end {equation}
La bulle se refroidit donc initialement moins vite que le milieu dès que la limite de Schwarzschild est enfoncée (c’est pourquoi elle devient moins dense que ce milieu). La bulle peut alors accélèrer très vite!
Bien entendu, les gaz ne se détendent pas de façon strictement adiabatique dans la zone de convection – en particulier parce que la température de la « bulle » ci-dessus diffère rapidement de celle de son environnement. Elle va donc échanger de la chaleur avec celui-ci, être elle-même déstabilisée et brassée (turbulence), ... ce qui va avoir tendance à réhomogénéiser le milieu. En fait, le raisonnement ci-dessus suggère qu’en régime convectif établi (stable), le profil de température ne peut s’écarter significativement du gradient thermique adiabatique :
\begin {equation} \frac {d}{dr}T(r)\approx T^\prime _c(r)=\left (1-\frac {1}{\gamma }\right )\frac {T(r)}{P(r)}\frac {d}{dr}P(r)=-\frac {g(r)}{C_\mathrm {p}}\,. \end {equation}
On supposera également que les écarts à l’équilibre hydrostatique dans la zone de convection ne sont pas suffisants pour remettre en cause les équations \eqref{eq:eqhydro1}–\eqref{eq:eqhydro4}.
L’épaisseur de la zone convective de surface varie d’une étoile à l’autre ; elle est d’environ \(0.25R_\odot \) pour le Soleil mais ne représente que \(\approx 2\%\) de sa masse (alors que la zone radiative comprend les 98% restants, coeur compris). L’épaisseur relative de cette zone convective tend à augmenter lorsque la masse de l’étoile diminue. Les étoiles les plus petites et « froides » sont ainsi entièrement convectives. A l’inverse, le coeur peut également devenir convectif et s’entourer d’une zone radiative dans les étoiles les plus lourdes de la séquence principale où domine le cycle CNO (car le débit d’énergie par unité d’angle solide \({\cal L}(r)/(4\pi r^2)\) y devient très grand, voir ci-dessous).
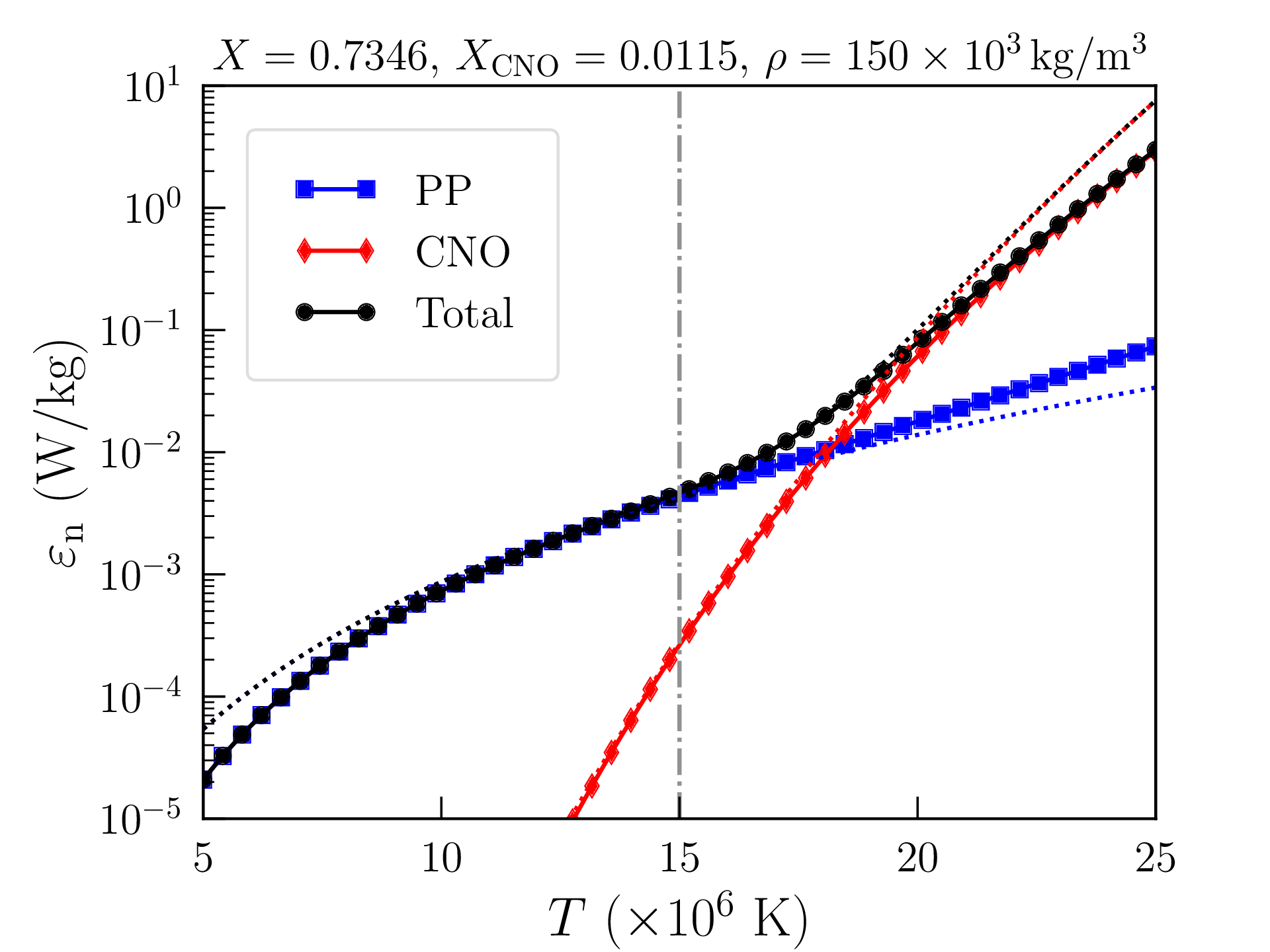
Le calcul de la section efficace des réactions nucléaires permet d’établir l’approximation suivante pour la puissance par unité de masse libérée par les chaînes proton-proton [10] :
\begin {equation} \varepsilon _\mathrm {n}=0.238\rho X^2 f_\mathrm {PP}\psi _\mathrm {PP}C_\mathrm {PP}T_6^{-2/3}\exp \left (-33.8T_6^{-1/3}\right )\,\text {W/kg} \label {eq:dmpPP} \end {equation}
avec \(T_6=T/(10^6\,\text {K})\), \(\rho \) en kg/m\(^3\), et :
\begin {align} f_\mathrm {PP}&=1+4.206\times 10^{-3}X^2\sqrt {(3+X)\rho }T_6^{-3/2} \nonumber \\ \psi _\mathrm {PP}&=1+1.412\times 10^8\left (\frac {1}{X}-1\right )\exp \left (-49.98T_6^{-1/3}\right ) \nonumber \\ C_\mathrm {PP}&=1+0.0123T_6^{1/3}+0.0109T_6^{2/3}+0.000938T_6\,. \end {align}
On obtient de même pour le cycle CNO :
\begin {equation} \varepsilon _\mathrm {n}=8.67\times 10^{20}\rho XX_\mathrm {CNO}C_\mathrm {CNO}T_6^{-2/3}\exp \left (-152.28T_6^{-1/3}\right )\,\text {W/kg} \label {eq:dmpCNO} \end {equation}
avec
\begin {equation} C_\mathrm {CNO}=1+0.0027T_6^{1/3}-0.00778T_6^{2/3}-0.000149T_6 \end {equation}
et \(X_\mathrm {CNO}\) la fraction massique de carbone, azote et oxygène dans le coeur de l’étoile (\(\approx 1.15\%\) dans le Soleil).
Processus \(\varepsilon _0\) (W/kg) \(T_0\) (K) \(p\) \(q\) Refs.
Chaîne proton-proton \((1.07\times 10^{-8})X^2\) \(10^7\) \(1\) \(4\) [11]
\((9.5\times 10^{-9})X^2\) \(10^7\) \(1\) \(4\) [12, 13]
Cycle CNO \((6.54\times 10^{-11})XX_\mathrm {CNO}\) \(10^7\) \(1\) \(20\) [11]
Réaction triple \(\alpha \) \((?)Y^3\) \(10^8\) \(2\) \(40\) [?]
On pourra alternativement utiliser les lois de puissance suivantes (plus simples mais moins précises) :
\begin {equation} \varepsilon _\mathrm {n}=\varepsilon _0\left (\frac {\rho }{\rho _0}\right )^p\left (\frac {T}{T_0}\right )^q\,, \label {eq:dmp} \end {equation}
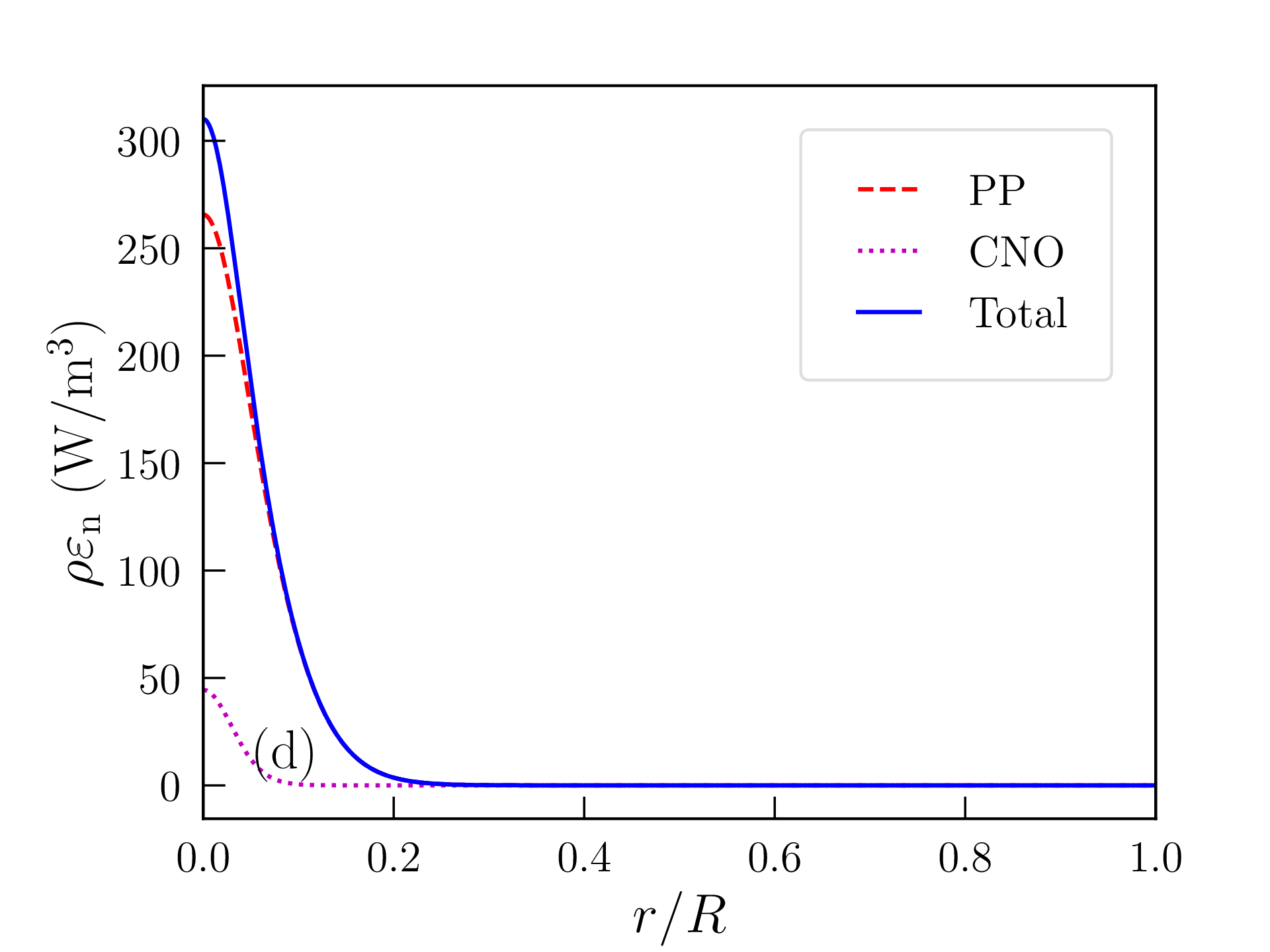
où \(\rho _0=1\)kg/m\(^3\) et les valeurs de \(\varepsilon _0\), \(T_0\), \(p\) et \(q\) sont reportées dans la table 2.1 pour différents processus de fusion (chaîne proton-proton, cycle CNO et réaction triple \(\alpha \)). Ces approximations sont comparées à \eqref{eq:dmpPP} et \eqref{eq:dmpCNO} sur la figure 2.4 (voir le code PPCNO.py). La densité de puissance \(\rho \varepsilon _\mathrm {n}\) est, logiquement, \(\propto \rho ^2\) pour les processus impliquant deux noyaux à la fois (fusion de l’hydrogène) et \(\propto \rho ^3\) pour la réaction triple \(\alpha \) impliquant « quasi-simultanément » trois particules (avec les fractions massiques correspondantes). En outre, le rendement des réactions CNO et triple \(\alpha \) est extrêmement dépendant de la température, avec des exposants \(q\) atteignant respectivement \(\approx 20\) et \(\approx 40\). La fusion reste cependant régulée au coeur de l’étoile tant que la matière n’est pas dégénérée : si les réactions nucléaires accélèrent, les gaz chauffent, la pression \(P\propto \rho kT\) augmente, si bien que coeur se détend et se refroidit, ce qui tempère in fine la réactivité. A l’inverse, si les réactions nucléaires ralentissent, la pesanteur contracte le coeur qui s’échauffe, ce qui relance la fusion. Ce mécanisme de contre-réaction n’existe pas dans un gaz dégénéré où la pression est indépendante de la température : les réactions nucléaires peuvent s’emballer et brûler des quantités impressionantes de combustible pour lever la dégénérescence (« flash de l’hélium » dans les étoiles évoluées), voir détruire l’astre (supernovas de type I dans les naînes blanches, voir chapitre 3).
La température \(T(r)\) et la densité de masse \(\rho (r)\) au sein de l’étoile vérifient donc (en première approximation) le système d’équations différentielles suivant :
\begin {equation} \frac {d}{dr}P(r)=\frac {d}{dr}[P_\mathrm {m}(r)+P_\mathrm {r}(r)]=-\rho (r)g(r)\text {\ (équilibre hydrostatique),} \label {eq:syntdPdr} \end {equation}
où :
\begin {align} &g(r)=\frac {G{\cal M}(r)}{r^2}\text {\ (accélération dans le champ de pesanteur de l'étoile),} \label {eq:syntg} \\ &{\cal M}(r)=4\pi \int _0^r dr^\prime \,r^{\prime 2}\rho (r^\prime )\text {\ (masse enclose dans la sphère de rayon $r$),} \label {eq:syntM} \\ &P_\mathrm {m}(r)=\frac {\rho (r)}{\mu }{\cal R}T(r)\text {\ (pression des gaz),} \label {eq:syntetat1} \\ &P_\mathrm {r}(r)=\frac {1}{3}aT(r)^4=\frac {4\sigma }{3c}T(r)^4\text {\ (pression radiative).} \label {eq:syntetat2} \end {align}
En outre,
\begin {equation} \frac {d}{dr}T(r)=\max \left (T^\prime _\mathrm {r}(r),T^\prime _\mathrm {c}(r)\right )\,, \label {eq:synthdTdr} \end {equation}
où :
\begin {align} T^\prime _\mathrm {r}(r)&=-\frac {3}{16\sigma }\frac {\rho (r)\kappa (r)}{T(r)^3}\frac {{\cal L}(r)}{4\pi r^2}\text {\ \ (gradient de transfert radiatif),} \label {eq:synthTpr} \\ T^\prime _\mathrm {c}(r)&=-\frac {g(r)}{C_\mathrm {p}}\text {\ \ (gradient thermique adiabatique en régime convectif),} \label {eq:synthTpc} \end {align}
avec \({\cal L}(r)\) le débit d’énergie dans l’étoile :
\begin {equation} {\cal L}(r)= 4\pi \int _0^r dr^\prime r^{\prime 2}\rho (r^\prime )\varepsilon _\mathrm {n}(r^\prime )\,, \label {eq:synthL} \end {equation}
et \(\varepsilon _\mathrm {n}(r)\) la puissance massique produite par les réactions thermonucléaires.
On utilise pour l’opacité \(\kappa (r)\) les lois de Kramers \eqref{eq:kappabf}–\eqref{eq:compton} ou les tables OPAL [9], et pour la puissance massique \(\varepsilon _\mathrm {n}(r)\) les équations \eqref{eq:dmpPP} et \eqref{eq:dmpCNO} ou leurs approximations \eqref{eq:dmp} avec les paramètres de la table 2.1.
Pour résoudre ce système, il faut appliquer des conditions aux limites appropriées. A cet effet, on suppose l’existence d’une surface hydrostatique caractérisée par une pression de référence \(P(R)=P_\mathrm {s}\), et on impose :
\({\cal M}(R)=M\), la masse totale de l’étoile.
\(T(R)=T_\mathrm {c}=L/(4\pi \sigma R^2)\), où \(L={\cal L}(R)\) est la luminosité de l’étoile (Loi de Stefan-Boltzmann).
On pourra alternativement caractériser la surface de l’étoile par une densité de référence \(\rho (R)=\rho _\mathrm {s}\) et imposer par conséquent :
\begin {equation} P_\mathrm {s}=\frac {{\cal R}}{\mu }\rho _\mathrm {s}T_\mathrm {c}+\frac {4\sigma }{3c}T_\mathrm {c}^4\,. \end {equation}
En pratique, la « surface visible » du soleil, appelée photosphère, est définie par des considérations optiques. Elle correspond à la zone où les gaz deviennent « optiquement fins11 » (transparents) et s’étend sur quelques centaines de kilomètres [14]. La densité moyenne dans la photosphère du Soleil, \(\rho _\mathrm {s}=3\times 10^{-4}\)kg/m\(^3\), est 4000 fois inférieure à la densité de l’air au niveau de la mer sur Terre. Par delà la photosphère s’étendent la chromosphère puis la couronne solaire. L’atmosphère (photosphère/chromosphère/couronne) des étoiles est un milieu très dilué et complexe12, structuré par les champs magnétiques, dont la description va bien au delà de l’approximation hydrostatique.
Il existe différentes façons de résoudre ce système d’équations différentielles (méthodes de type Newton-Raphson, ...). La plus simple consiste à trouver itérativement son point fixe « auto-cohérent » en utilisant une méthodes de différences finies pour intégrer les équations (voir le code star.py).
Il convient tout d’abord de remarquer que la pression et la température (donc toutes les quantités thermodynamiques) sont des fonctionnelles de la densité de masse \(\rho (r)\). On peut en effet calculer la pression \(P[\rho ](r)\) à partir des équations pour \({\cal M}(r)\), \(g(r)\) et \(dP/dr\). On obtient ensuite \(T[\rho ](r)\) en inversant l’équation d’état \(P(r)=P_\mathrm {m}(r)+P_\mathrm {r}(r)\equiv P(\rho (r),T(r))\) du gaz parfait.
On introduit la variable \(x=r/R\in [0, 1]\) et un maillage \(x_i\) (\(0\le i\le N\)) de cet intervalle avec \(x_0=0\) et \(x_N=1\). On fait l’approximation suivante pour les intégrales sur ce maillage :
\begin {equation} \int _0^{x_iR} dr\,4\pi r^2 f(r)=R^3\left [\sum _{j=0}^{i-1}f_j(\omega ^<_j+\omega ^>_j)+f_i\omega ^<_i\right ]\,, \end {equation}
où \(f_i=f(x_iR)\) et
\begin {align} &\omega ^<_0=0,\,\omega _{i\ne 0}^<=\frac {4\pi }{3}\left [x_i^3-\left (\frac {x_{i-1}+x_i}{2}\right )^3\right ] \\ &\omega ^>_{i\ne N}=\frac {4\pi }{3}\left [\left (\frac {x_{i+1}+x_i}{2}\right )^3-x_i^3\right ]\,,\omega ^>_N=0 \end {align}
sont les volumes normalisés des coquilles \(x\in [\tfrac {1}{2}(x_{i-1}+x_i), x_i]\) et \(x\in [x_i,\tfrac {1}{2}(x_{i-1}+x_i)]\) situées de part et d’autre de \(x=x_i\). On substitue par ailleurs aux équations différentielles des différences finies :
\begin {equation} \frac {d}{dr}F(r)=f(r)\Rightarrow F_{i+1}-F_i=\frac {R}{2}\left (x_{i+1}-x_i\right )\left (f_i+f_{i+1}\right )\,, \end {equation}
avec une condition aux limites appropriée pour \(F_0\) ou \(F_N\).
Partant d’une solution approchée \(\rho _i^{(n)}\) pour la densité de masse sur le maillage, on calcule \({\cal M}_i^{(n)}\), \(g_i^{(n)}\) puis \(P_i^{(n)}\) à partir de \eqref{eq:syntdPdr}, \eqref{eq:syntM} et \eqref{eq:syntg}. On en déduit alors la température \(T_i^{(n)}\) en inversant les équations d’état \eqref{eq:syntetat1} et \eqref{eq:syntetat2}, et le débit d’énergie \({\cal L}_i^{(n)}\) à partir de \eqref{eq:synthL}. On injecte ensuite ces quantités dans l’équation \eqref{eq:synthdTdr} pour \(dT/dr\) que l’on intègre pour obtenir un nouveau profil de température \(T_i^{(n+1)}\) et un nouveau profil de densité de masse
\begin {equation} \rho _i^{(n+1)}=\frac {\mu }{\cal R}\left [\frac {P_i^{(n)}}{T_i^{(n+1)}}-\frac {4\sigma }{3c}\left (T_i^{(n+1)}\right )^3\right ] \end {equation}
à partir, une fois encore, des équations d’état \eqref{eq:syntetat1} et \eqref{eq:syntetat2}. On ajuste enfin le rayon \(R\) de l’étoile de sorte que
\begin {equation} \int _0^{R} dr\,4\pi r^2 \rho (r)=M=R^3\sum _{i=0}^{N}\rho _i^{(n+1)}(\omega ^<_i+\omega ^>_i)\,, \end {equation}
et on itère jusqu’à convergence de la densité de masse :
\begin {equation} \left |\rho ^{(n+1)}-\rho ^{(n)}\right |=\sqrt {\sum _i\left (\rho _i^{(n+1)}-\rho _i^{(n)}\right )^2}<\varepsilon \,. \end {equation}
Ce processus itératif converge en principe vers un point fixe solution des équations \eqref{eq:syntdPdr}–\eqref{eq:synthL}. Toutefois, les oscillations de \(\rho ^{(n)}\) d’une itération à l’autre peuvent entraver la convergence si elles ne sont pas amorties. C’est pourquoi il est judicieux de tempérer les variations de la densité de masse en « mélangeant » les solutions \(\rho ^{(n)}\) et \(\rho ^{(n+1)}\) avant d’itérer :
\begin {equation} \rho _i^{(n+1)}\leftarrow \alpha \rho _i^{(n+1)}+(1-\alpha )\rho _i^{(n)}\,, \end {equation}
où \(\alpha \sim 0.2\) assure en pratique la convergence pour toute masse \(M\in [0.1M_\odot , 50M_\odot ]\).
On peut partir de la solution homogène \(\rho _i^{(0)}=3M/(4\pi R^3)\) avec \(R=R_\odot \sqrt {M/M_\odot }\) (voir paragraphes 2.2.3 et 2.5.3). On applique à chaque itération les conditions aux limites :
\begin {align} P_N^{(n)}&=\frac {{\cal R}}{\mu }\rho _sT_N^{(n)}+\frac {4\sigma }{3c}\left (T_N^{(n)}\right )^4 \\ T_N^{(n+1)}&=\left (\frac {{\cal L}_N^{(n)}}{4\pi \sigma R^2}\right )^{1/4}\,. \end {align}
On obtient ainsi les profils de densité de masse, température, pression, et débit d’énergie pour une masse \(M\) donnée.
On peut résoudre à l’aide du code star.py le système d’équations \eqref{eq:syntdPdr}–\eqref{eq:synthL} pour le Soleil avec les paramètres suivants [1, 5] :
Masse \(M_\odot =1.99\times 10^{30}\)kg.
Composition homogène \(X_\odot =0.7346\), \(Y_\odot =0.2485\), \(Z_\odot =0.0169\), et \(X_\mathrm {CNO}=0.0115\).
Tables OPAL pour l’opacité \(\kappa (\rho ,T)\) [9].
Capacité calorifique isobare par particule \(c_\mathrm {p}=5k/2\).
Densité de surface \(\rho _\mathrm {s}=3\times 10^{-4}\)kg/m\(^3\).
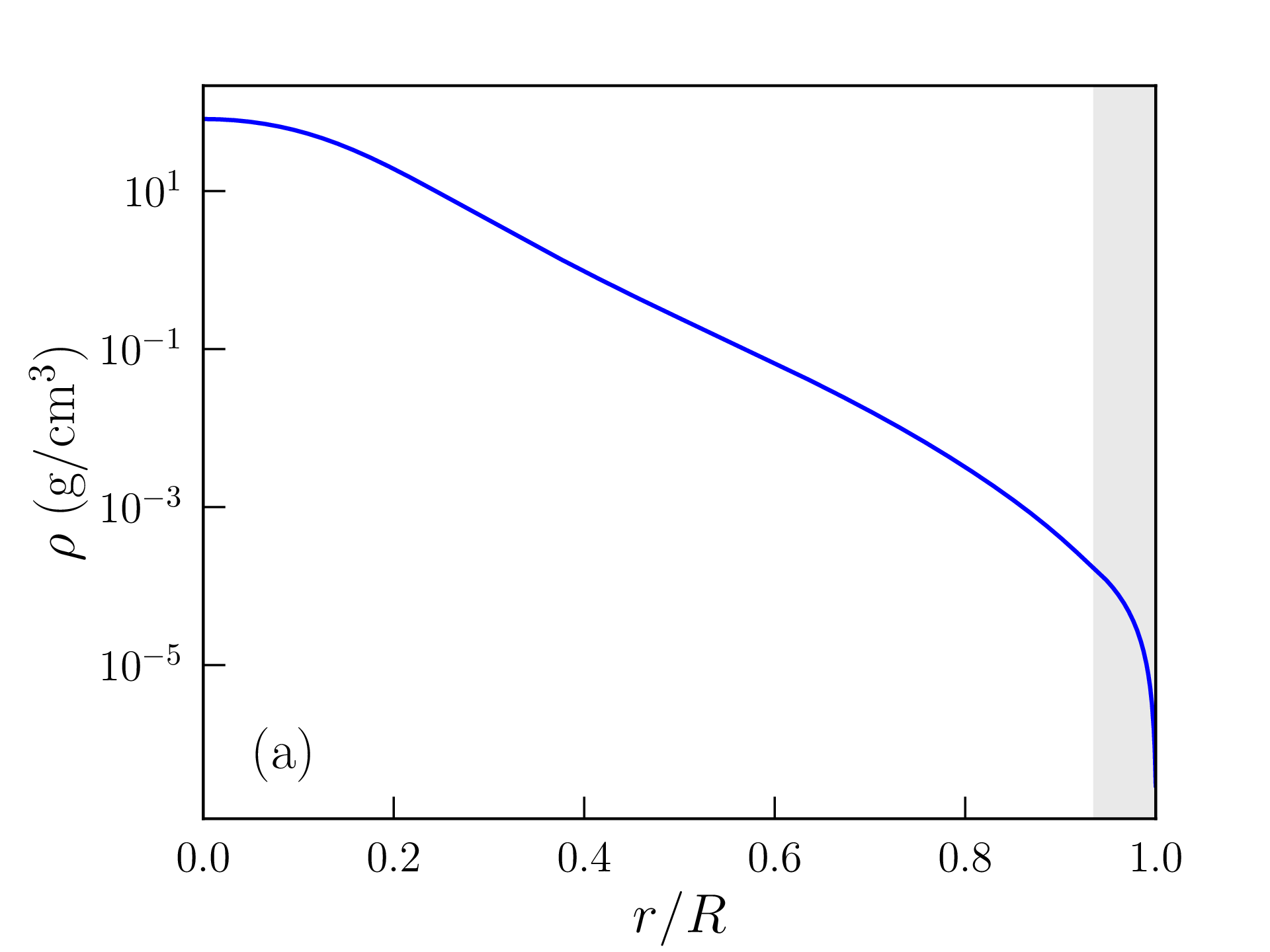
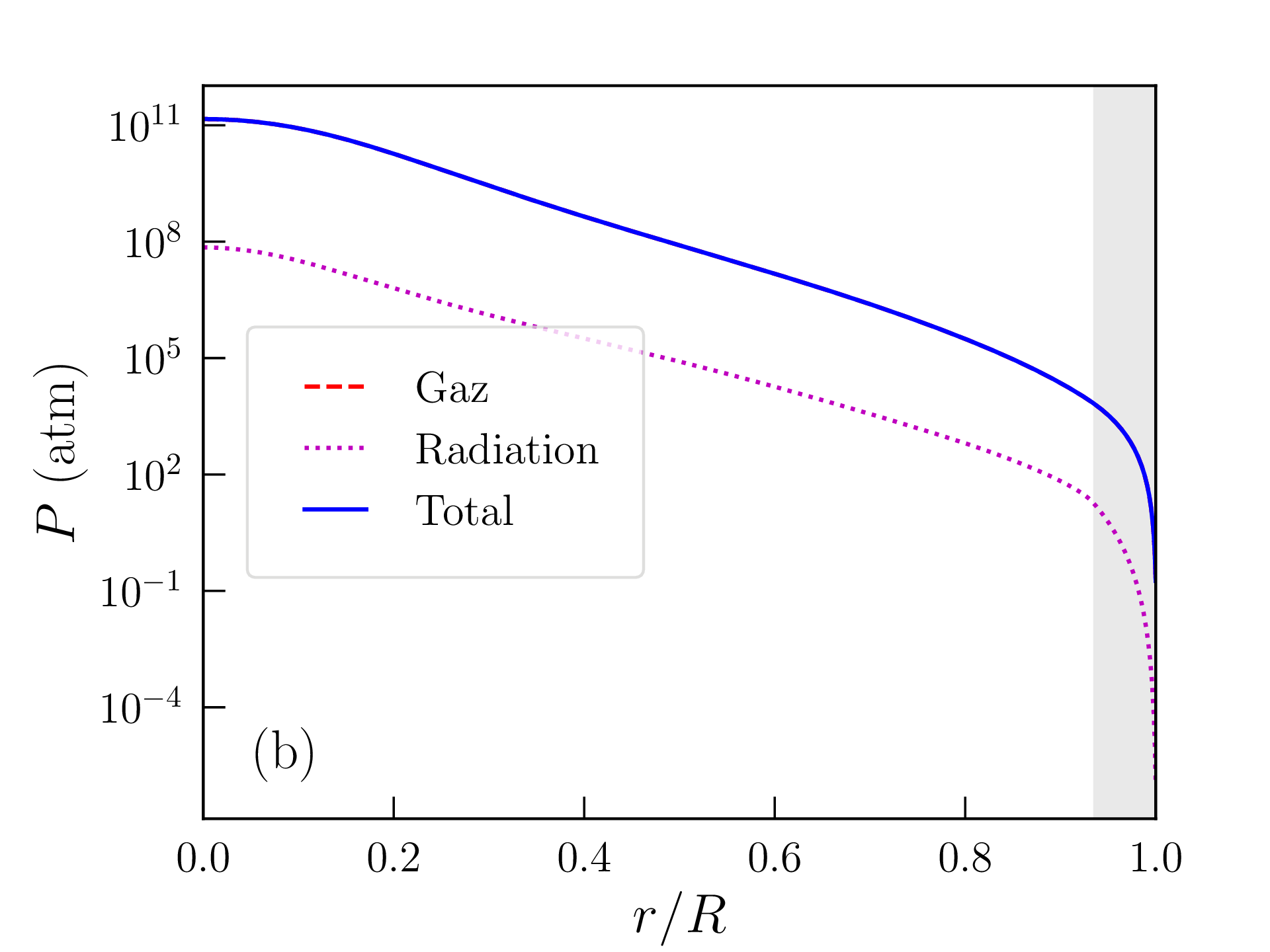
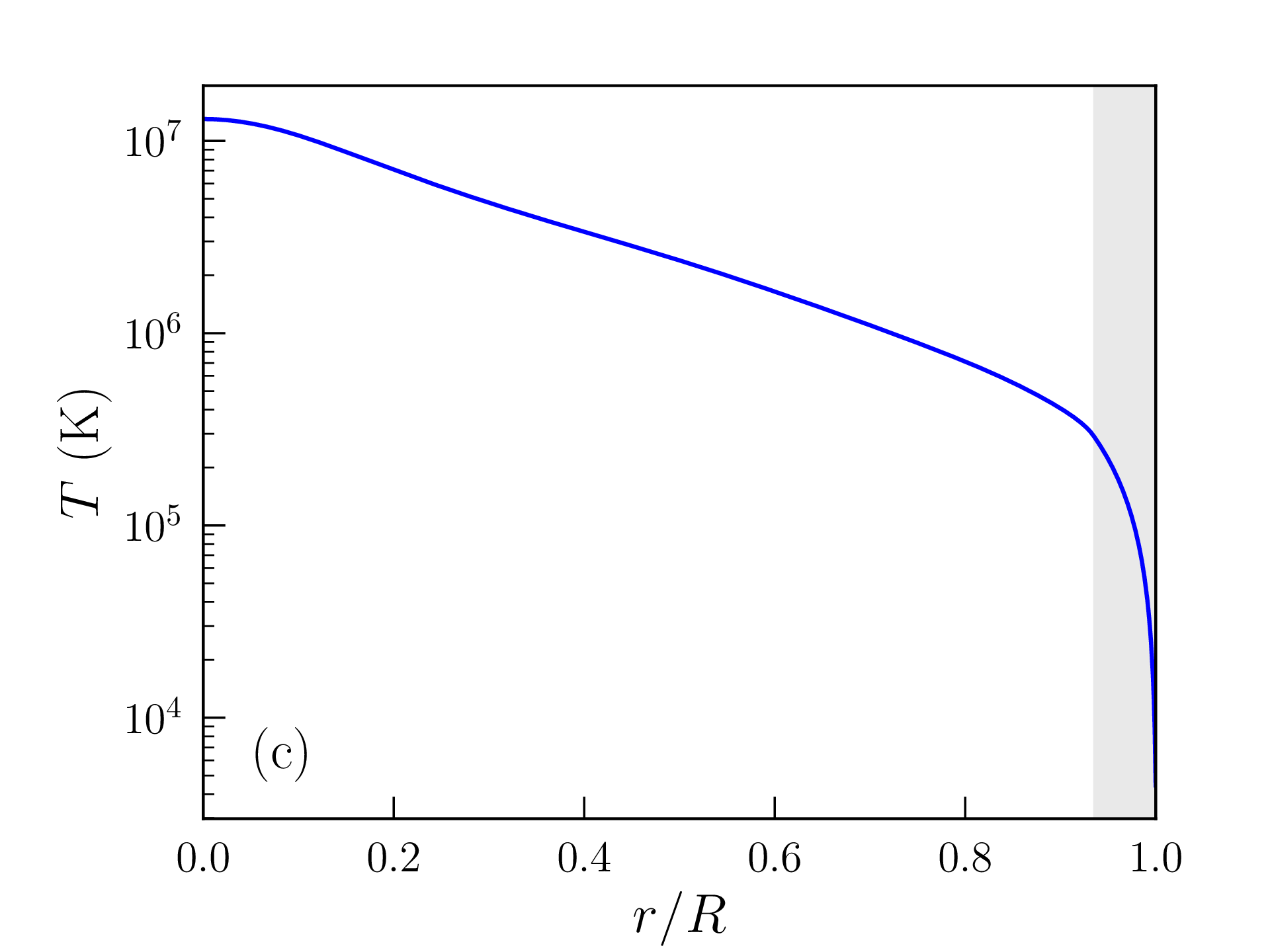
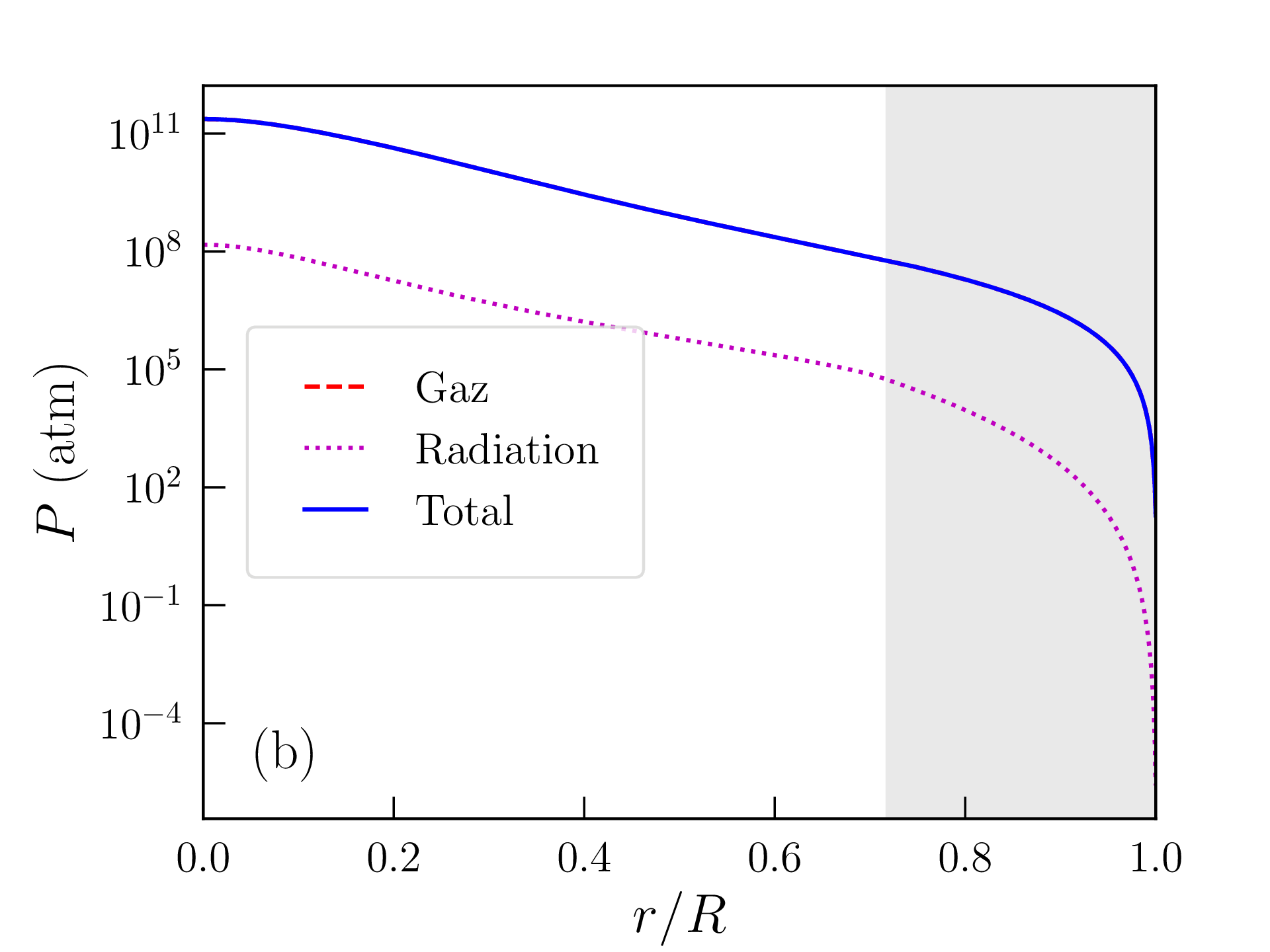
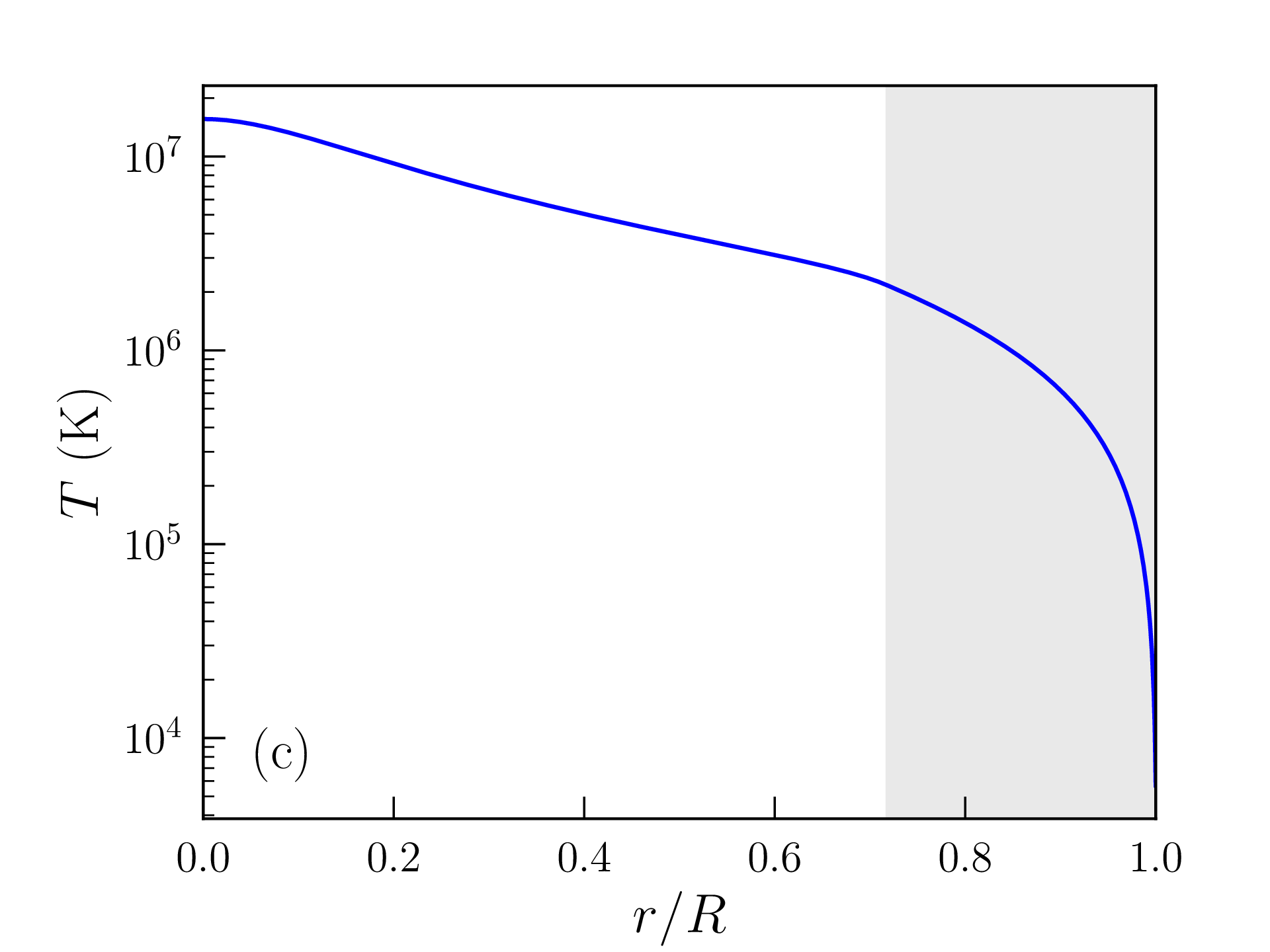
Les profils de densité de masse, pression, température, densité d’énergie produite par les réactions nucléaires, et libre parcours moyen des photons ainsi obtenus sont représentés sur la figure 2.6. Les grandeurs caractéristiques du Soleil (rayon, luminosité...) calculées avec ce modèle « homogène » sont reportées dans la table 2.2 et comparées aux mesures ou estimations astronomiques. La solution obtenue est peu satisfaisante à bien des égards :
L’étoile est beaucoup trop grande (\(R=930\,006\) km au lieu de \(R_\odot =696\,340\) km).
Sa luminosité est bien trop faible (\(L=2.4\times 10^{26}\) W au lieu de \(L_\odot =3.83\times 10^{26}\) W).
La densité de masse, la pression et la température centrale sont largement sous-estimées.
Le libre parcours moyen des photons atteint le mètre avant que ne démarre la convection ; la zone de convection à la surface de l’étoile est trop fine.
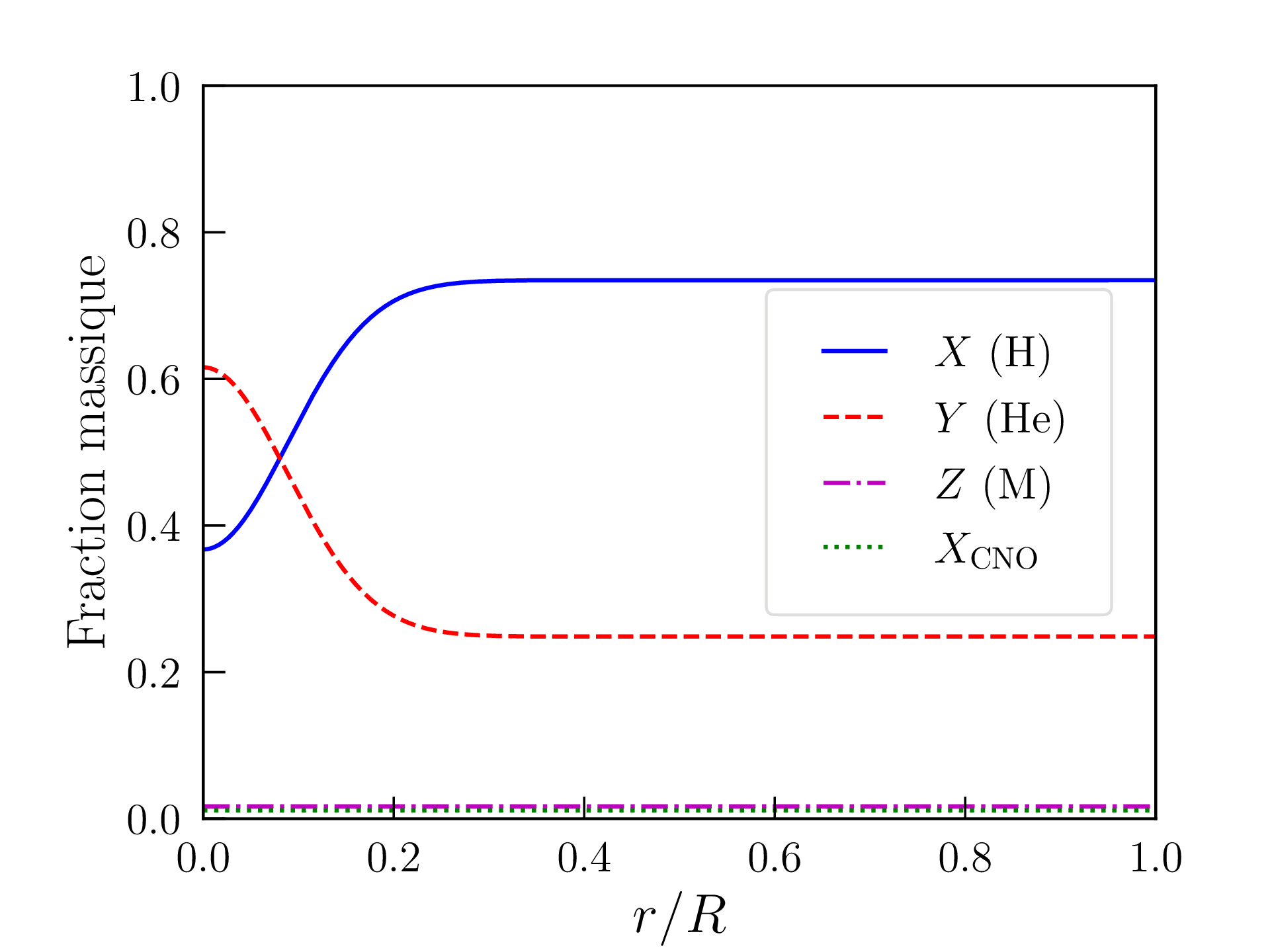
Ces carences résultent des hypothèses effectuées ainsi que des limites intrinsèques du modèle. Tout d’abord, la composition du Soleil est loin d’être homogène. Il brille en effet depuis 4.5 milliards d’années, aussi son coeur s’est-il déjà considérablement enrichi en hélium : on estime en effet que \(X\approx 0.36\) et \(Y\approx 0.62\) au centre du Soleil. On obtient de bien meilleurs résultats pour la densité de masse, la pression et la température centrales avec le profil de composition (empirique) suivant, représenté sur la figure 2.5 :
\begin {equation} X(r)=X_\odot \left (1-\frac {1}{2}e^{-\left (\tfrac {r}{0.125R}\right )^2}\right )\,. \label {eq:composition} \end {equation}
En outre, l’épaisseur de la zone de convection, donc la taille de l’étoile dépendent énormément de la condition aux limites choisie pour \(P(R)\) ou \(\rho (R)\). En effet, la loi de Laplace \eqref{eq:Laplace2} s’applique dans toute la zone de convection étant données les approximations effectuées :
\begin {equation} T(r)^\gamma P(r)^{1-\gamma }=\mathrm {Constante}=T(R)^\gamma P(R)^{1-\gamma }\,. \end {equation}
où \(\gamma =5/3\) est le coefficient adiabatique du gaz13. Par conséquent, le choix de \(P(R)\) (et de \(\gamma \)!) contraint fortement le profil de pression et de température dans la zone de convection. En l’absence d’un modèle d’atmosphère stellaire permettant de calculer un \(P_\mathrm {s}\) ou \(\rho _\mathrm {s}\) effectif pour la surface hydrostatique, il est donc difficile de trouver une solution pertinente des équations \eqref{eq:syntdPdr}–\eqref{eq:synthL} si seule la masse \(M\) de l’étoile est connue. Il convient de se donner un deuxième paramètre, telle que le rayon, la luminosité ou la température de surface par exemple afin de fixer \(P_\mathrm {s}\) ou \(\rho _\mathrm {s}\) en conséquence. Dans le cas présent, on obtient un bon accord avec les données astronomiques en choisissant :
\begin {equation} \rho _\mathrm {s}=2.5\times 10^{-2}\,\text {kg/m}^3\,. \label {eq:rhos} \end {equation}
Cette valeur est certes bien supérieure à la densité de masse moyenne dans la photosphère solaire, mais il faut garder à l’esprit que les hypothèses faites dans la zone de convection et à la surface de l’étoile sont assez grossières. La densité de masse calculée varie, en particulier, d’un ordre de grandeur tous les \(\approx 2500\) km au voisinage de cette surface. Les profils de densité de masse, pression, température, densité d’énergie produite et libre parcours moyen des photons obtenus avec ce modèle « inhomogène » sont représentés sur la figure 2.7 et les grandeurs caractéristiques correspondantes reportées dans la table 2.2. L’accord avec les données astronomiques est très satisfaisant mais les choix \eqref{eq:composition} et \eqref{eq:rhos} restent empiriques. Comme attendu d’une étoile de cette masse, la pression de radiation est négligeable et la fusion nucléaire est largement dominée par les chaînes proton-proton. Le rayon et la masse du coeur, défini comme la région qui produit 99% de la luminosité, atteignent respectivement \(\approx 0.25R_\odot \) et \(0.5M_\odot \). L’essentiel de la masse du Soleil est donc contenue dans son noyau. Le libre parcours moyen des photons dans la zone radiative ne dépasse pas quelques millimètres et la température atteint encore \(T\approx 2\times 10^6\)K à l’entrée de la zone de convection (appelée tachocline).
Rayon \(R_\odot \) (km) \(930\,006\) \(691\,366\) \(696\,340\)
Densité moyenne \(\overline {\rho }\) (g/cm\(^3\)) \(0.59\) \(1.44\) \(1.41\)
Densité centrale \(\rho (0)\) (g/cm\(^3\)) \(81.62\) \(151.40\) \(\approx 150\)
Champ de pesanteur en surface \(g(R)\) (m/s\(^2\)) \(153.6\) \(277.9\) \(274\)
Température de surface \(T_\mathrm {c}\equiv T(R)\) (K) \(4444\) \(5698\) \(5775\)
Température centrale \(T(0)\) (\(10^6\) K) \(13.0\) \(15.6\) \(\approx 15.1\)
Pression centrale \(P(0)\) (\(10^9\) atm) \(145.0\) \(233.9\) \(\approx 225\)
Luminosité \(L_\odot \) (\(10^{26}\) W) \(2.40\) \(3.59\) \(3.83\)
dont cycle CNO (%) \(0.10\) \(2.09\) \(\lesssim 2\)
Epaisseur de la zone de convection (\(R_\odot \)) \(0.065\) \(0.283\) \(\approx 0.25\)
Masse de la zone de convection (\(M_\odot \)) \(\approx 0\) \(0.026\) \(\approx 0.02\)
Rayon du coeur @\(0.99L_\odot \) (\(R_\odot \)) \(0.206\) \(0.263\) \(\approx 0.25\)
Masse du coeur @\(0.99L_\odot \) (\(M_\odot \)) \(0.524\) \(0.509\) \(\approx 0.50\)
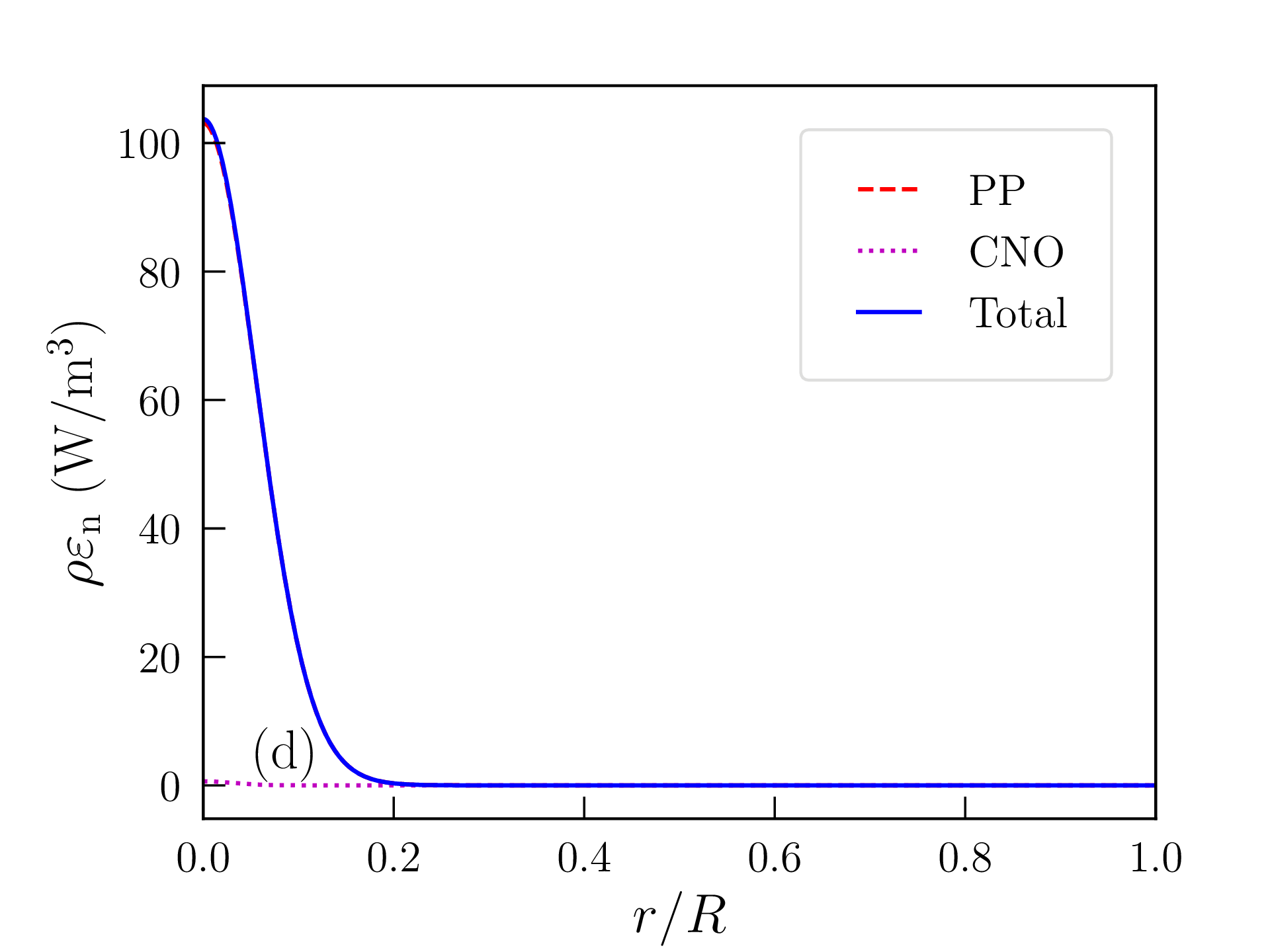
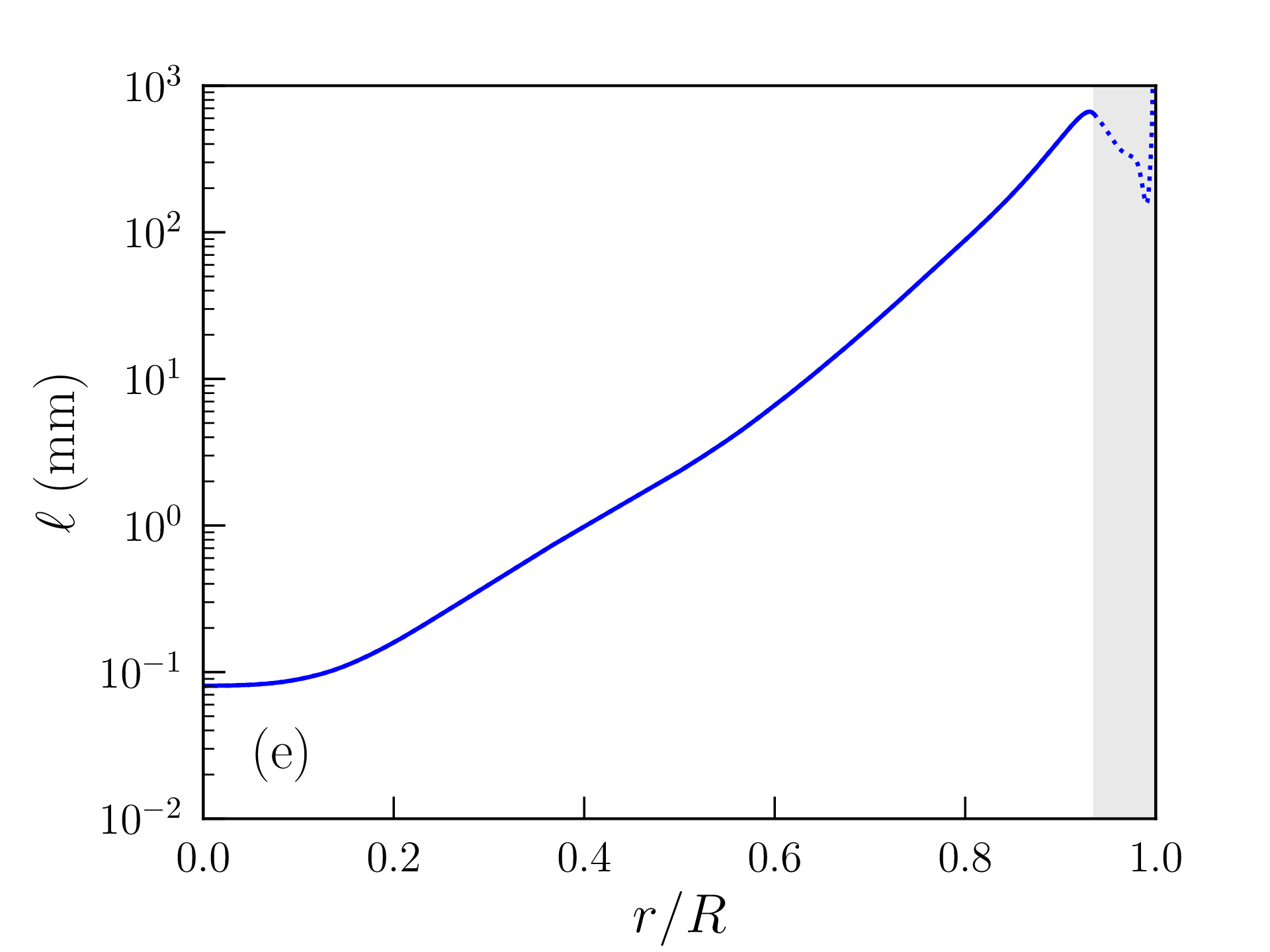
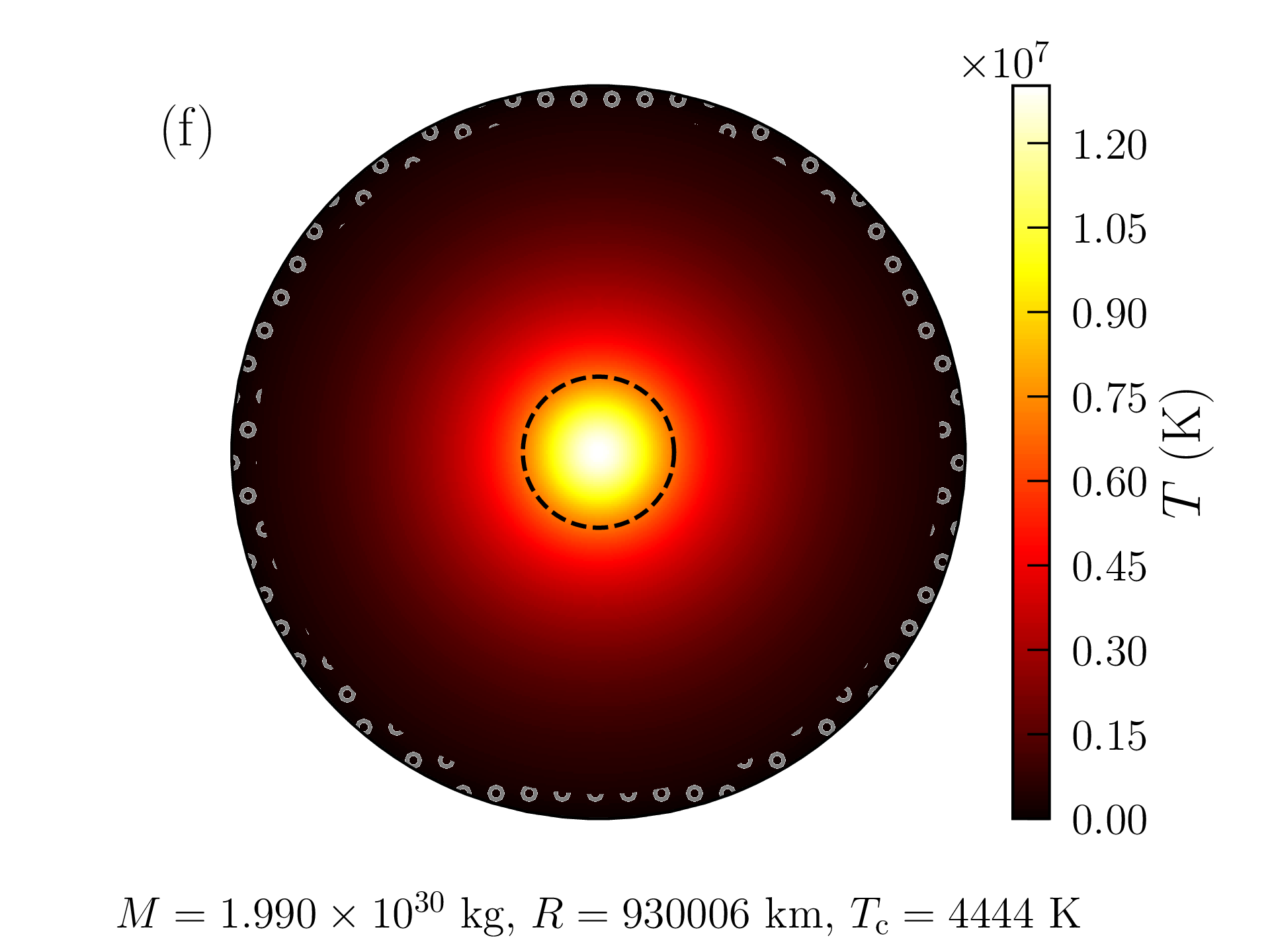
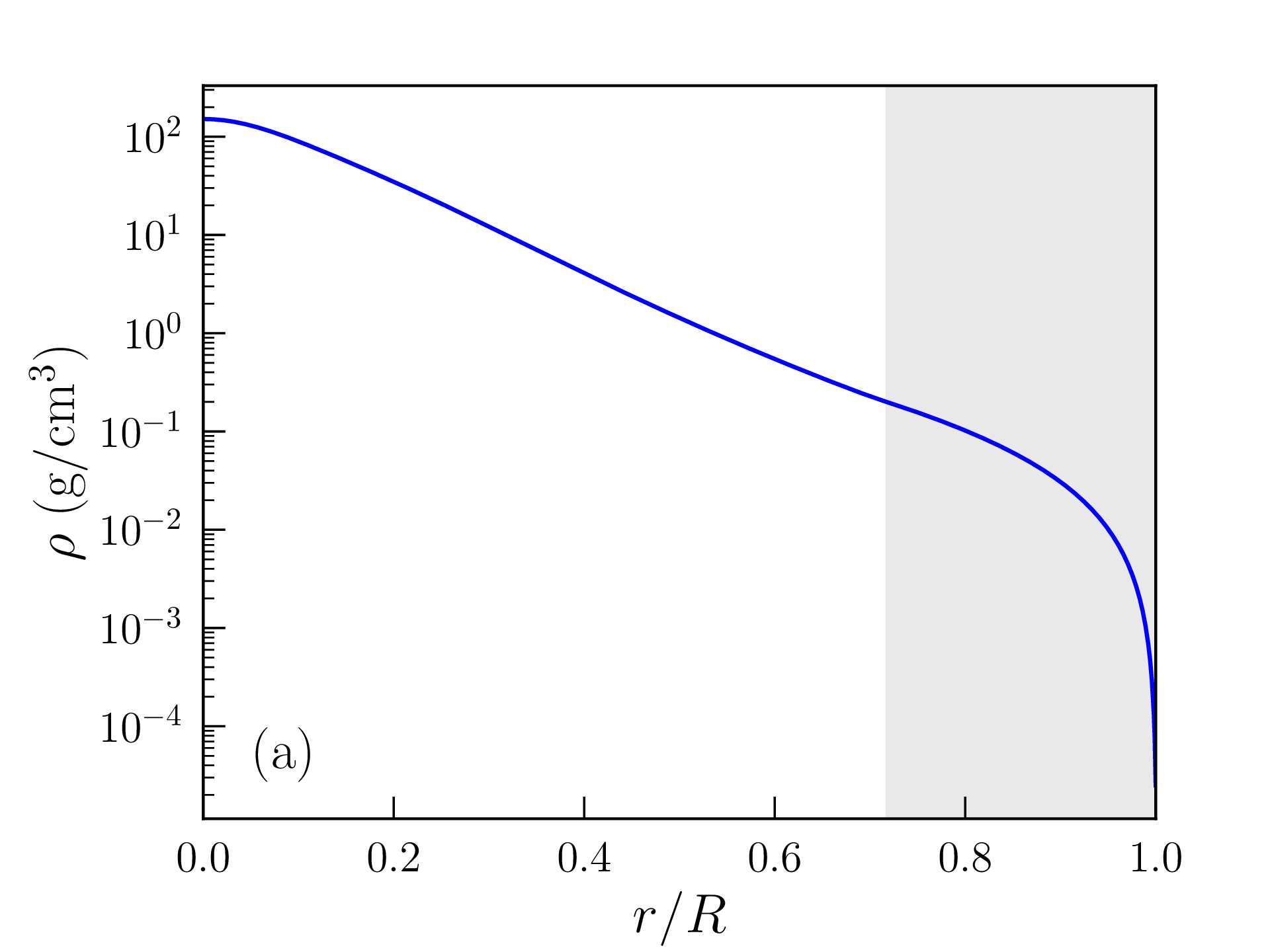
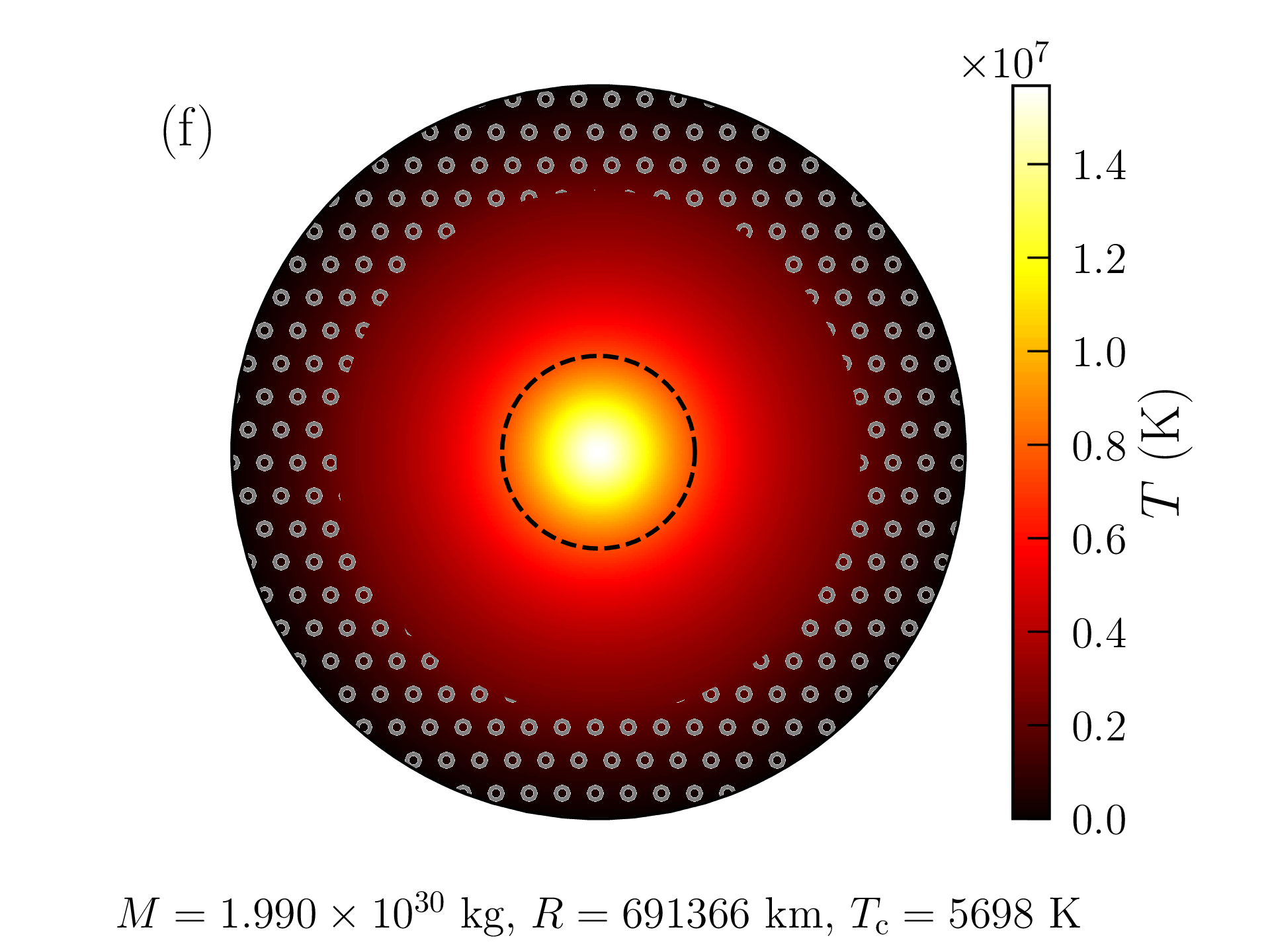
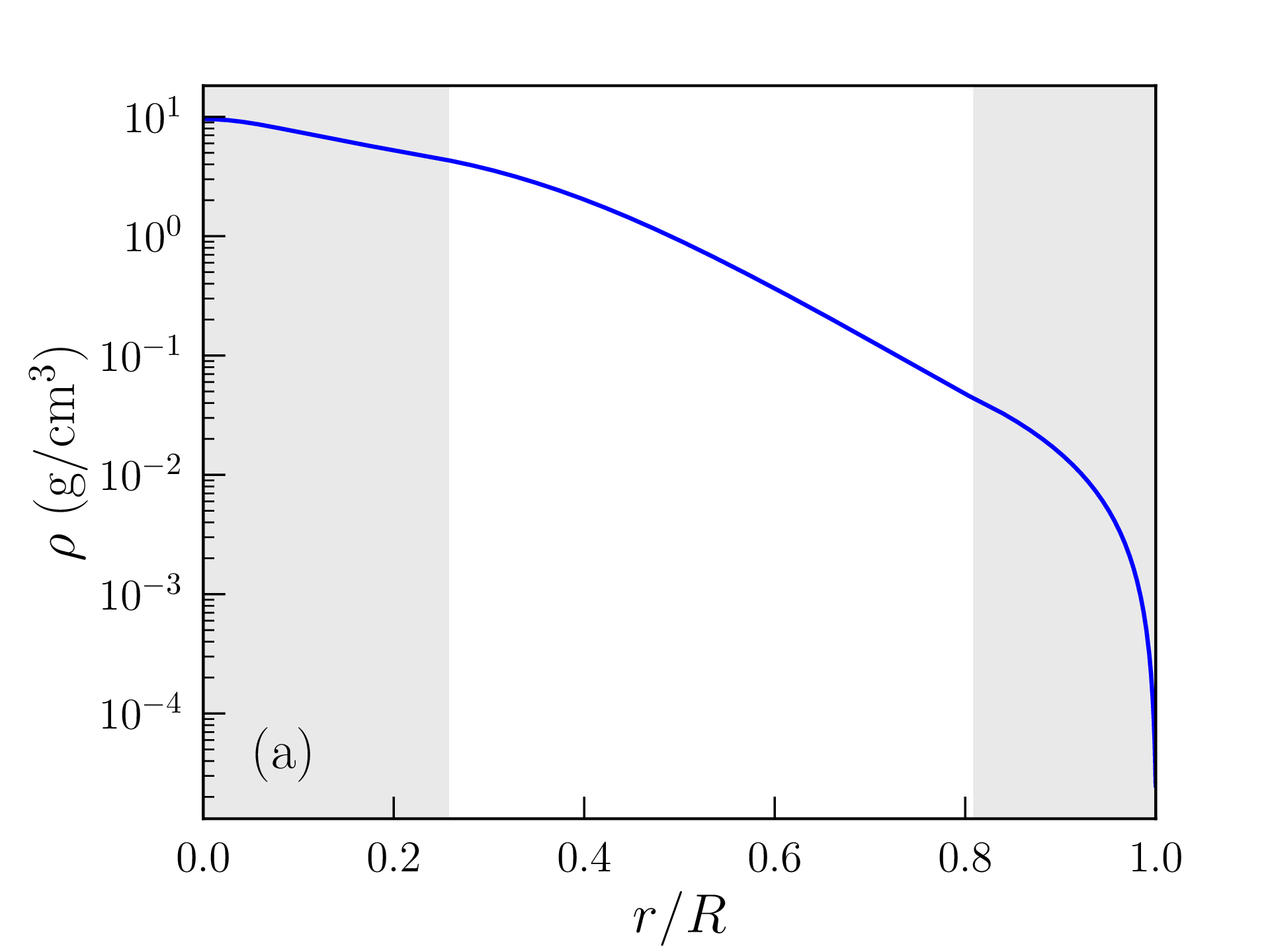
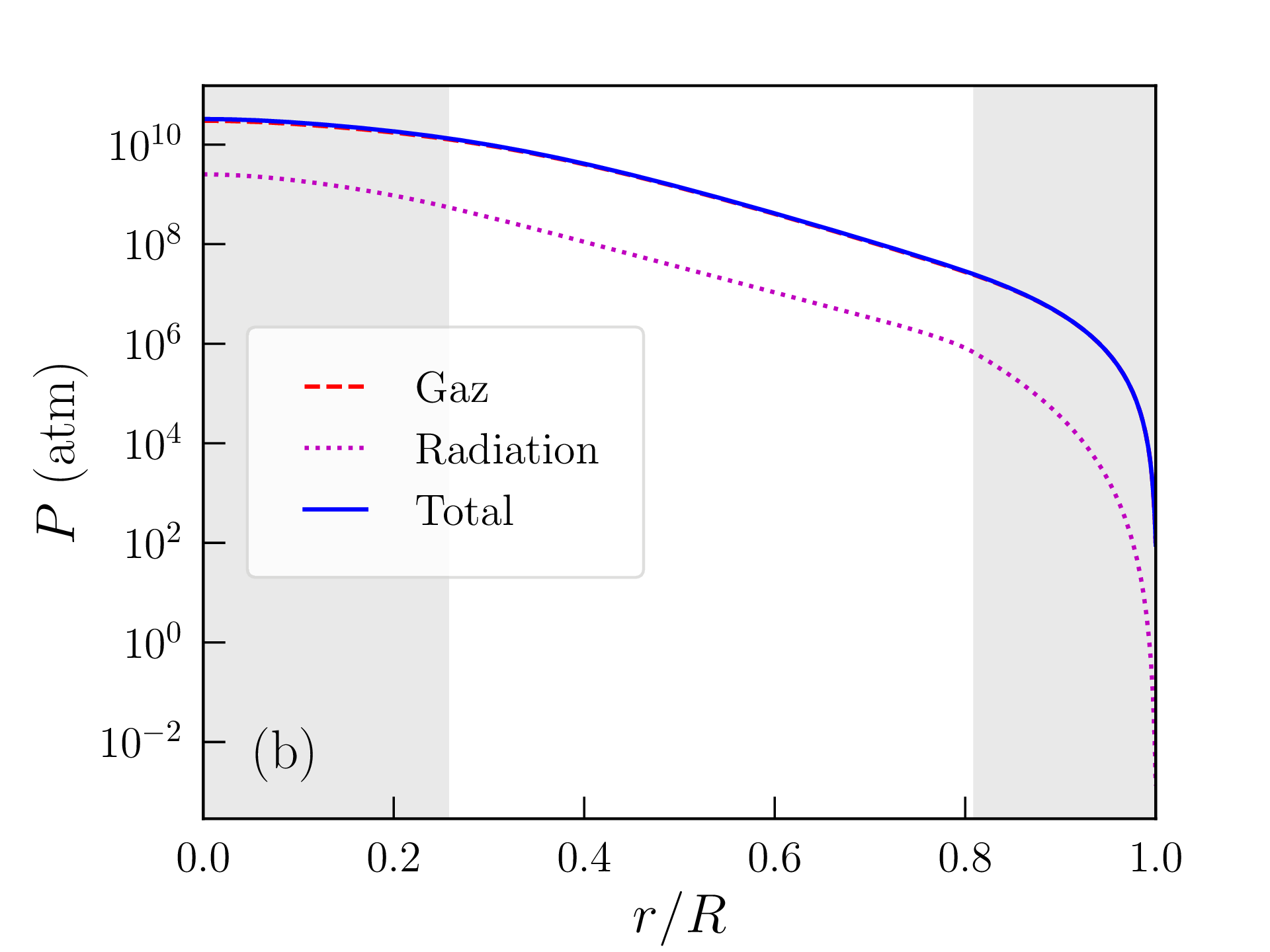
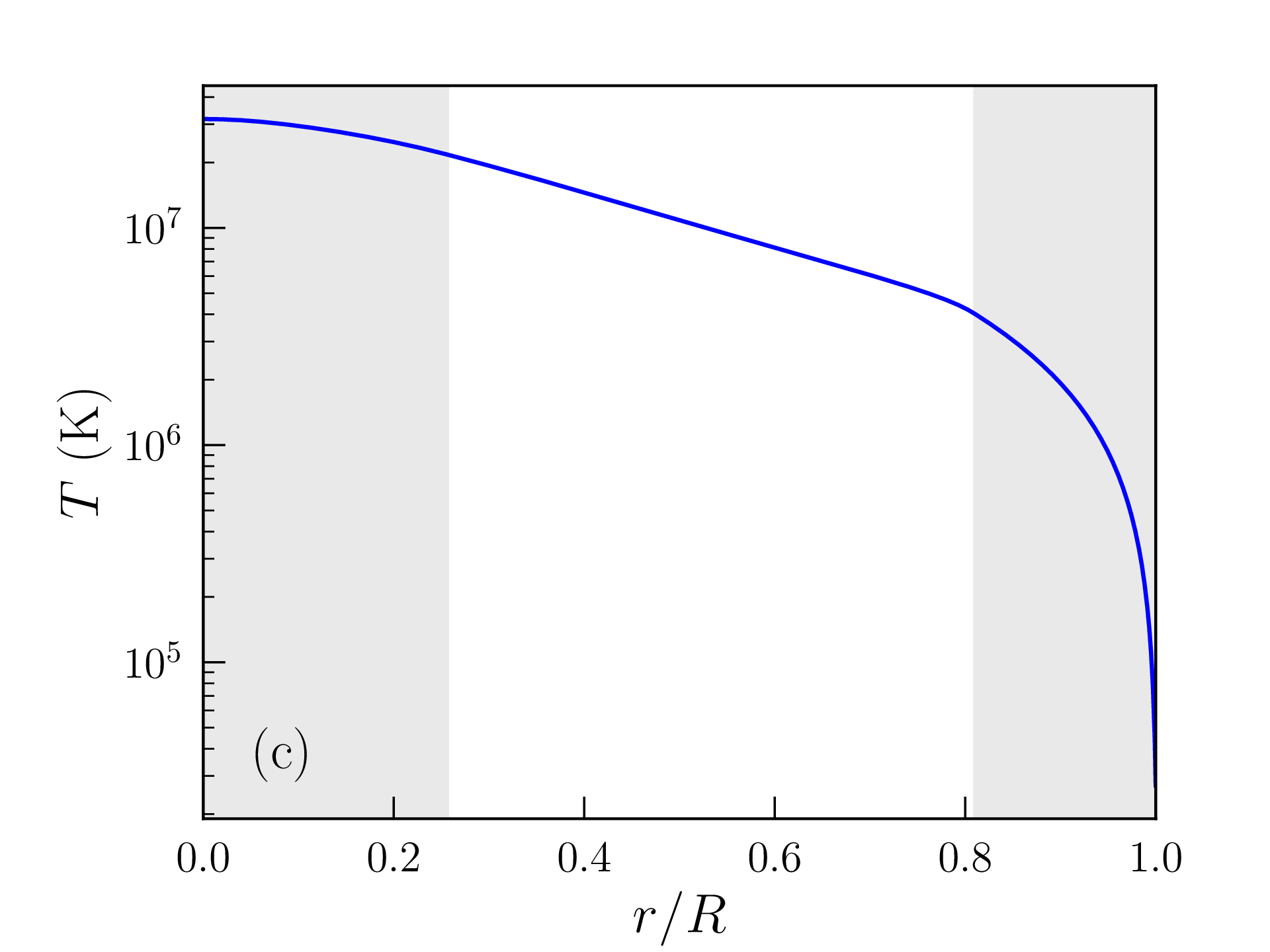
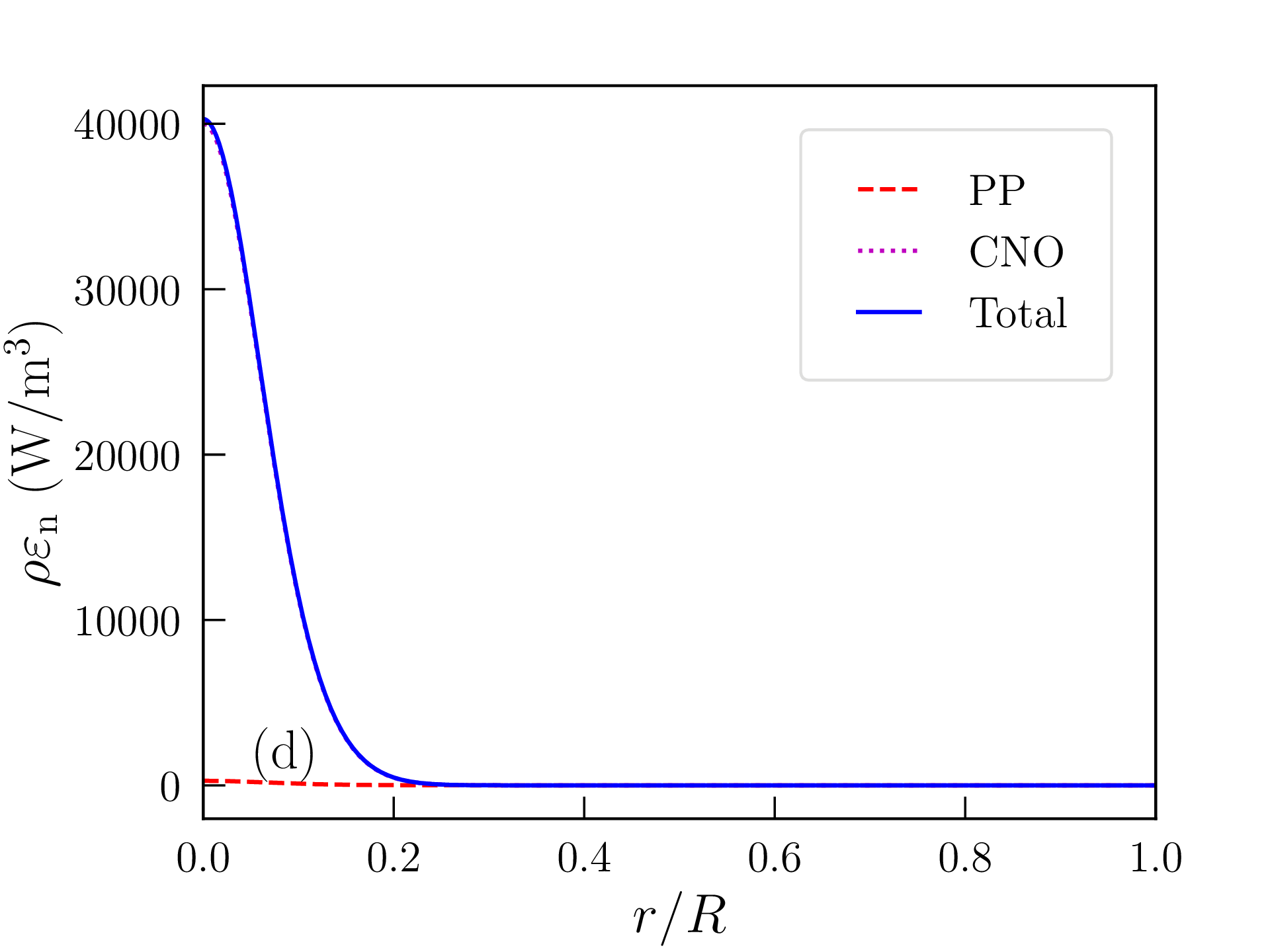
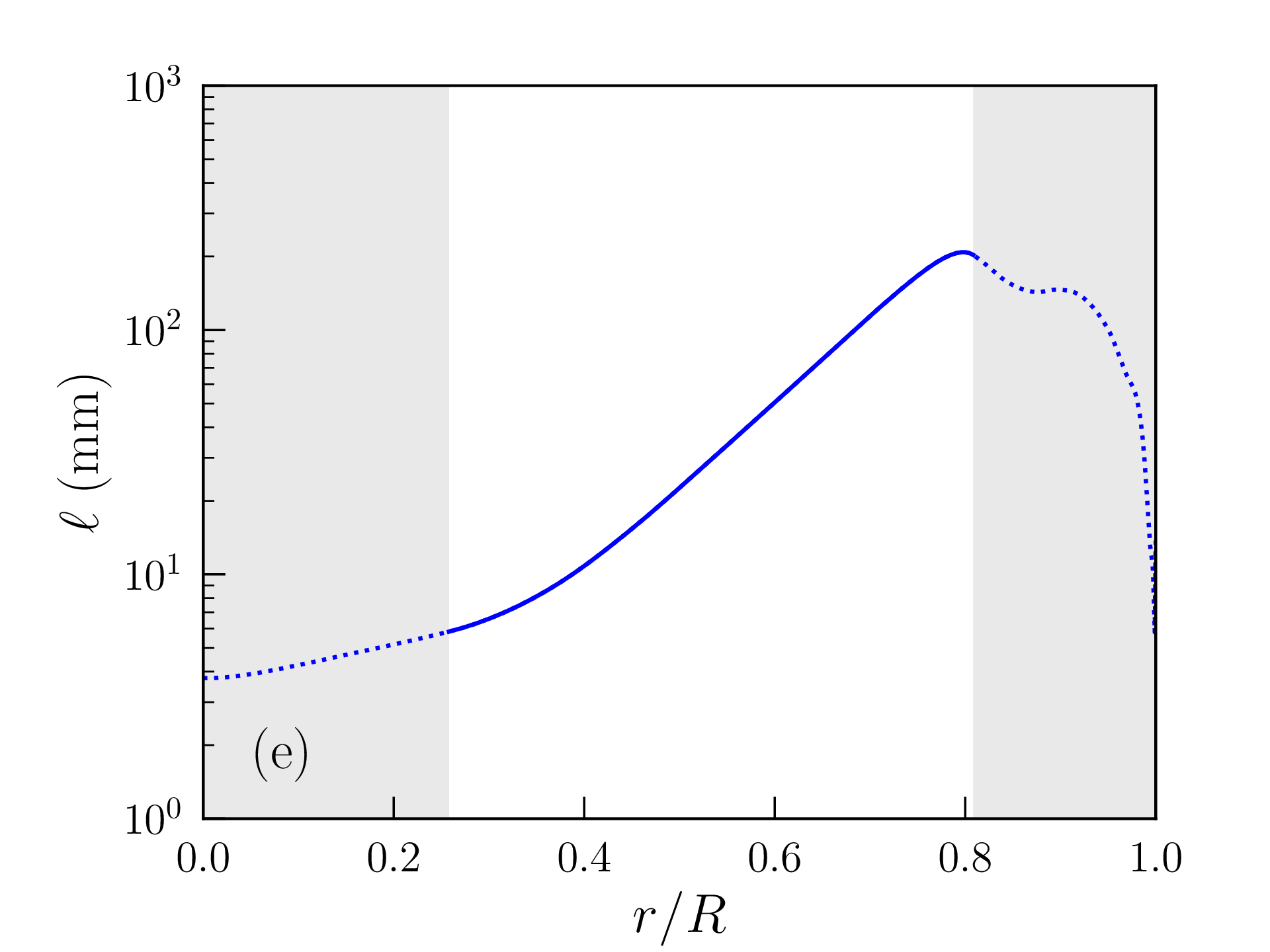
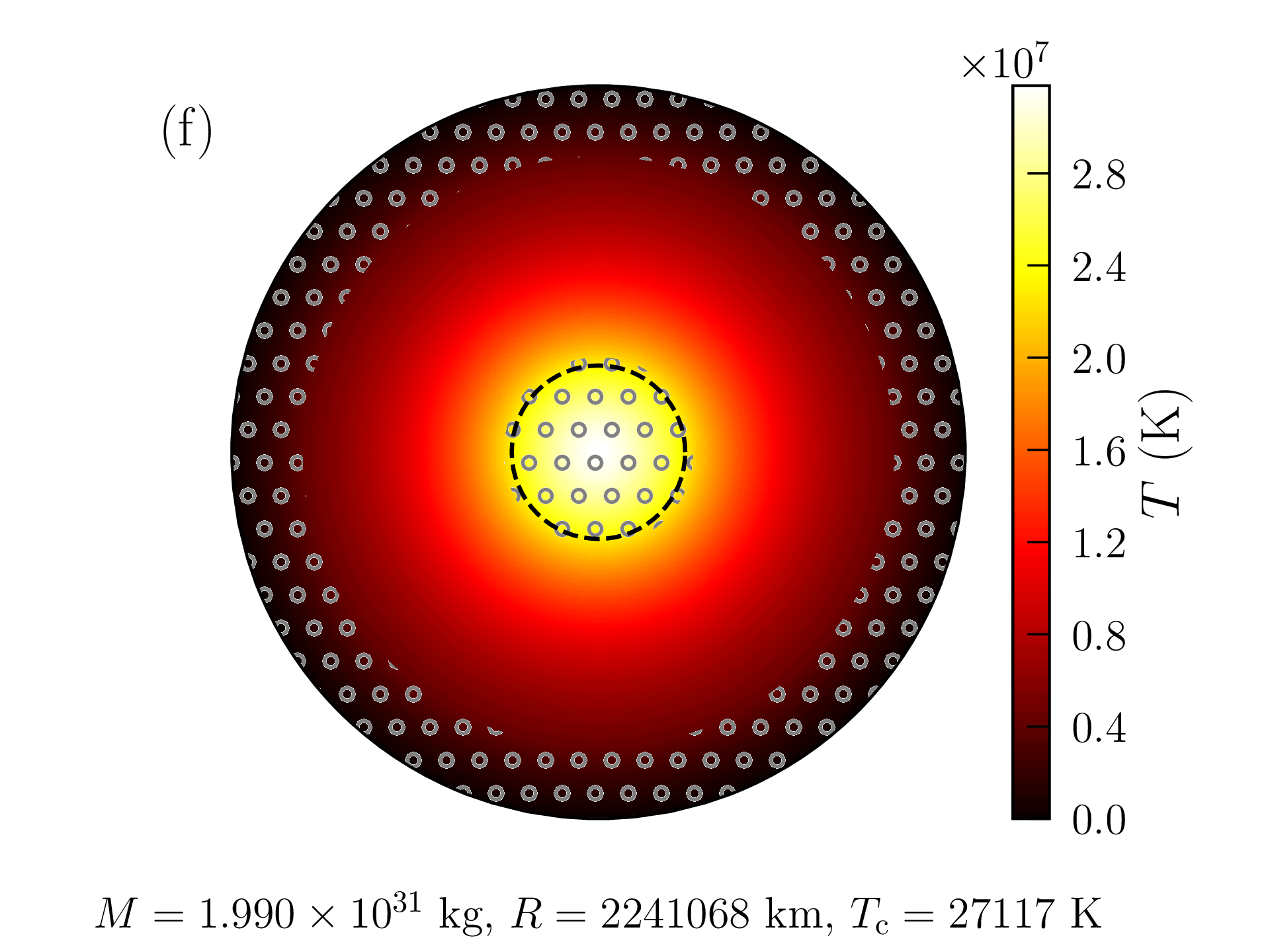
Les profils obtenus pour une étoile de masse \(M=10M_\odot \) [avec les mêmes hypothèses de composition \eqref{eq:composition} et de densité de surface \eqref{eq:rhos}] sont représentés à titre indicatif sur la figure 2.8 (car il faudrait vraisemblablement ajuster aussi bien le profil de composition que \(\rho _\mathrm {s}\) ou \(P_\mathrm {s}\)). La profondeur relative de la zone de convection en surface a diminué, mais le coeur lui-même est devenu convectif14 et les réactions de fusion sont maintenant dominées par le cycle CNO. Le rayon de l’étoile atteint \(R=2\,241\,068\)km et sa luminosité \(L=1.94\times 10^{30}\)W est presque 5000 fois supérieure à celle du Soleil. Sa surface est également beaucoup plus chaude (\(T_\mathrm {c}=27\,117\)K). La température centrale atteint \(T(0)=31.7\times 10^6\)K ; la pression centrale \(P(0)=32.6\times 10^9\)atm et la densité centrale \(\rho (0)=9.6\)g/cm\(^3\) sont cependant plus faibles que dans le Soleil.
Le modèle est beaucoup moins réaliste pour des étoiles de faible masse \(M<0.5M_\odot \) qui ne sont pas assez convectives et trop froides. Ces carences peuvent résulter, d’une part, de l’approximation \eqref{eq:dmpPP} pour la densité massique d’énergie produite par les réactions nucléaires, moins précise pour \(T<10^7\)K, et, d’autre part, de la description simpliste de la zone de convection qui domine le transfert d’énergie dans ces étoiles (et qui nécessiterait une approche hydrodynamique plus rigoureuse).
Les équations \eqref{eq:syntdPdr}–\eqref{eq:synthL} permettent d’établir quelques relations générales sur la structure et la luminosité des étoiles.
Les équations \eqref{eq:syntdPdr}–\eqref{eq:synthL} imposent une limite à la pression radiative (donc à la luminosité) que peut supporter une étoile. En effet, puisque \(P_\mathrm {r}(r)=4\sigma T(r)^4/(3c)\),
\begin {equation} \frac {d}{dr}P_\mathrm {r}(r)=\frac {16\sigma }{3c}{T(r)^3}\frac {d}{dr}T(r)\,. \label {eq:Edd1} \end {equation}
Dans la zone radiative, on a ainsi :
\begin {equation} \frac {d}{dr}P_\mathrm {r}(r)=-\frac {1}{c}\rho (r)\kappa (r)\frac {{\cal L}(r)}{4\pi r^2}\,. \label {eq:Edd2} \end {equation}
En outre,
\begin {equation} \frac {d}{dr}P(r)=\frac {d}{dr}P_\mathrm {m}(r)+\frac {d}{dr}P_\mathrm {r}(r)=-\rho (r)g(r)\,, \label {eq:Edd3} \end {equation}
et :
\begin {equation} \frac {d}{dr}P_\mathrm {m}(r)=\frac {{\cal R}}{\mu }\left (\rho (r)\frac {d}{dr}T(r)+T(r)\frac {d}{dr}\rho (r)\right )\,. \end {equation}
D’après \eqref{eq:Edd1} et \eqref{eq:Edd2}, \(dP_\mathrm {r}(r)/dr<0\) donc \(dT(r)/dr<0\) ; par conséquent \(dP_\mathrm {m}(r)/dr<0\) sinon \(d\rho (r)/dr>0\) : l’étoile, instable, expulse son enveloppe. Toutes les dérivées de \eqref{eq:Edd3} sont ainsi négatives, de sorte que :
\begin {equation} \frac {d}{dr}P_\mathrm {r}(r)\Big /\frac {d}{dr}P(r)=\frac {1}{c}\frac {\kappa (r)}{g(r)}\frac {{\cal L}(r)}{4\pi r^2}=\frac {1}{4\pi cG}\kappa (r)\frac {{\cal L}(r)}{{\cal M}(r)}<1\,. \end {equation}
On doit donc partout avoir dans la zone radiative :
\begin {equation} {\cal L}(r)<\frac {4\pi cG{\cal M}(r)}{\kappa (r)}\,. \end {equation}
On obtient une borne supérieure pour la luminosité \(L\) de l’étoile en remplaçant \({\cal M}(r)\) par la masse totale \(M\) de l’étoile et \(\kappa (r)\) par sa valeur minimale \(\kappa _\mathrm {m}\approx 0.04\)m\(^2\)/kg dans un plasma d’hydrogène pur soumis à la seule diffusion Compton \eqref{eq:compton} par les électrons :
\begin {equation} L<L_\mathrm {Edd}=\frac {4\pi cGM}{\kappa _\mathrm {m}}\,. \label {eq:Eddington} \end {equation}
C’est la « limite d’Eddington » à la luminosité d’une étoile de masse \(M\) :
\begin {equation} L_\mathrm {Edd}\approx (1.26\times 10^{31} \text {\ W})\frac {M}{M_\odot }\,, \end {equation}
ou équivalemment :
\begin {equation} \frac {L_\mathrm {Edd}}{L_\odot }\approx 3.3\times 10^4\frac {M}{M_\odot }\,. \end {equation}
Les équations \eqref{eq:syntdPdr}–\eqref{eq:synthL} avec leurs conditions aux limites lient implicitement le rayon et la luminosité de l’étoile à sa masse totale (théorème de Vogt-Russell). Elles suggèrent donc qu’il existe une relation univoque entre la masse de l’étoile et sa luminosité à paramètres du modèle constants (\(\mu \), \(C_\mathrm {p}\), \(\varepsilon _\mathrm {n}\), \(\kappa \)). On peut dégager une loi d’échelle en écrivant la densité de masse :
\begin {equation} \rho (r)=\frac {3M}{4\pi R^3}f\left (\frac {r}{R}\right )\,, \label {eq:rhored} \end {equation}
où \(f(x)\) est une fonction adimensionnelle définie sur l’intervalle \(x\in [0,1]\), telle que :
\begin {equation} M=4\pi \int _0^R dr\,r^2\rho (r)=3M\int _0^1 dx\,x^2f(x)\Rightarrow \int _0^1 dx\,x^2f(x)=\frac {1}{3}\,. \end {equation}
En particulier, \(f(x)=1\) pour une distribution de masse homogène. On a alors :
\begin {equation} {\cal M}(r\le R)=4\pi \int _0^r dr\,r^2\rho (r)=3MF_1\left (\frac {r}{R}\right )\,, \end {equation}
où :
\begin {equation} F_1(x)=\int _0^x du\,u^2f(u)\,, \end {equation}
est également une fonction adimensionnelle (comme tous les \(F_n\) introduits ci-dessous). Par conséquent,
\begin {equation} \frac {dP}{dr}(r\le R)=-\rho \frac {G{\cal M}(r)}{r^2}=G\frac {M^2}{R^5}F_2\left (\frac {r}{R}\right )\,. \end {equation}
Si la pression reste dominée par la matière,
\begin {equation} \frac {d}{dr}P(r)=\frac {{\cal R}}{\mu }\left (\rho (r)\frac {d}{dr}T(r)+T(r)\frac {d}{dr}\rho (r)\right )\,, \label {eq:dPdrscal} \end {equation}
de sorte que :
\begin {equation} T(r)=\frac {\mu G}{{\cal R}}\frac {M}{R}F_3\left (\frac {r}{R}\right )\,. \label {eq:dTdrscal2} \end {equation}
Enfin, en supposant \(\kappa \) constant,
\begin {align} {\cal L}(r)&=-\frac {64\pi \sigma }{3\rho (r)\kappa (r)}r^2T(r)^3\frac {d}{dr}T(r) \nonumber \\ &=\frac {\sigma }{\kappa }\left (\frac {\mu G}{{\cal R}}\right )^4M^3F_4\left (\frac {r}{R}\right )\,. \end {align}
Masse et luminosité devraient donc suivre la loi d’échelle :
\begin {equation} L\equiv {\cal L}(R)\propto M^3\,. \end {equation}
En pratique, on mesure plutôt :
\begin {equation} \frac {L}{L_\odot }\propto \left (\frac {M}{M_\odot }\right )^\alpha \,, \label {eq:relationML} \end {equation}
avec \(\alpha \approx 3.5\) sur la séquence principale (voir Fig. 2.9)15. Les étoiles les plus lourdes, où le cycle CNO domine la fusion, s’écartent par le bas de cette tendance, alors qu’à l’inverse, les étoiles les plus légères, où prévaut la convection, s’en écartent pas le haut. Cette relation peut-être utilisée pour estimer la masse d’une étoile dont on a pu mesurer la magnitude absolue.
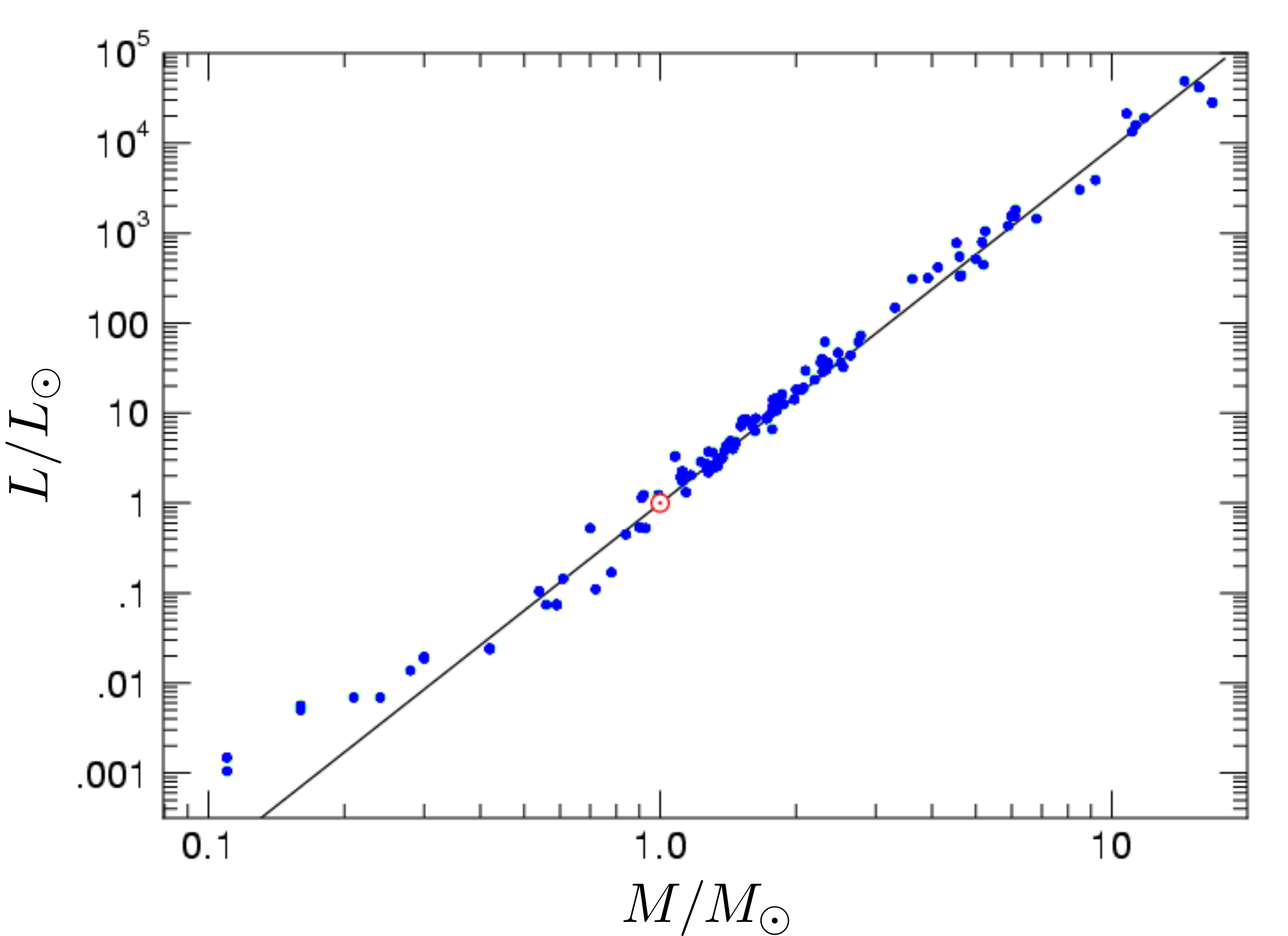
En outre, la relation masse-luminosité \eqref{eq:relationML} et la luminosité d’Eddington \eqref{eq:Eddington} imposent une limite à la masse des étoiles, au delà de laquelle elles sont déstabilisées par la pression de radiation :
\begin {equation} M<\left (\frac {4\pi cG}{\kappa _\mathrm {m}}\frac {M_\odot ^\alpha }{L_\odot }\right )^\frac {1}{\alpha -1}\approx 65M_\odot \,. \end {equation}
Il faut cependant prendre garde aux nombreuses approximations faites dans la dérivation de ces expressions (hypothèse hydrostatique, exposant \(\alpha \) indépendant de la masse...). Il existe de rares étoiles plus massives que cette limite, qui sont de fait assez instables et qui expulsent de grandes quantités de matière au cours de leur (bref) passage par la séquence principale.
Enfin, le « potentiel » thermonucléaire d’une étoile étant naturellement proportionnel à sa masse, son durée de vie moyenne sur la séquence principale varie comme :
Il doit de même exister une relation masse/rayon pour les étoiles de la séquence principale ; puisque
\begin {equation} L=4\pi R^2\sigma T_\mathrm {c}^4\,, \end {equation}
où \(T_\mathrm {c}\equiv T(R)\) est la température de couleur de l’étoile, il doit aussi exister une relation entre \(T_\mathrm {c}\) et la masse, ou encore une relation entre \(L\) et \(T_\mathrm {c}\). Le diagramme \(L\) vs \(T_\mathrm {c}\) est appelé diagramme de Hertzprung-Russel (voir Fig. 2.10). Il permet de classer les étoiles par type spectral (couleur) et luminosité (deux quantités plus faciles à mesurer que la masse). La grande majorité des étoiles, qui passent l’essentiel de leur vie sur la séquence principale, forme une bande bien visible sur ce diagramme. Les différents types spectraux sont identifiés par une lettre (M, K, G, F, A, B, O du rouge au bleu, voir table 2.3).
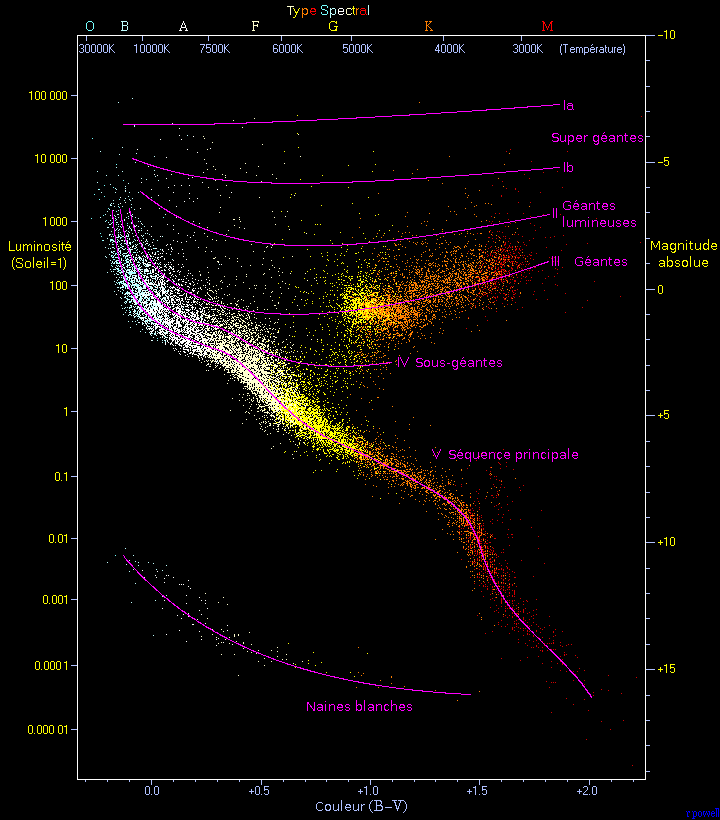
Comme sur ce diagramme \(L\propto T_\mathrm {c}^6\) sur la séquence principale, et que \(L\propto R^2T_\mathrm {c}^4\propto M^3\), on en déduit empiriquement16 \(T_\mathrm {c}\propto R\) et \(R\propto \sqrt {M}\). Les étoiles en dehors de la séquence principale sont sauf exception des étoiles évoluées (branche des géantes) qui ne brûlent plus de l’hydrogène qu’en coquille et/ou brûlent des éléments plus lourds que l’hydrogène (He, C, ...) dans le noyau, voir des cadavres stellaires (naînes blanches).
Type Température Couleur
O \(>25\,000\)K Bleue B \(10\,000-25\,000\) K Bleue-blanche
A \(7\,500-10\,000\)K Blanche F \(6\,000-7\,500\) K Jaune-blanche
G \(5\,000-6\,000\)K Jaune (Soleil)
K \(3\,500-5\,000\)K Orange
M \(<3\,500\)K Rouge
1.Ce n’est pas nécessairement vrai pour les atomes « métalliques » (numéro atomique \(Z>2\)) qui possèdent plus d’électrons, ni près de la surface de l’étoile, plus froide.
2.On introduit également l’indice de métallicté :
\begin {equation} [\mathrm {M}/\mathrm {H}]=\log _{10}\frac {N_\mathrm {M}/N_\mathrm {H}}{(N_\mathrm {M}/N_\mathrm {H})_\odot }\approx \log _{10}\frac {Z}{Z_\odot }\,, \nonumber \end {equation}
où \(N_\mathrm {M}\) et \(N_\mathrm {H}\) sont les abondances atomiques des métaux et de l’hydrogène dans l’étoile, et \((N_\mathrm {M}/N_\mathrm {H})_\odot \) est leur rapport dans la photosphère solaire. La métallicité est représentative de l’âge et de la génération d’une étoile, les éléments métalliques provenant en général de l’enrichissement préalable du milieu interstellaire par des supernovas. Les étoiles les plus vieilles (population II) sont très pauvres en métaux, alors que les étoiles les plus jeunes (population I) sont plus riches.
3.C’est approximativement le cas pour les principaux métaux : C (\(m_\mathrm {*}\simeq 12m_\mathrm {H}\), \(p_\mathrm {*}=7\)), N (\(m_\mathrm {*}\simeq 14m_\mathrm {H}\), \(p_\mathrm {*}=8\)), O (\(m_\mathrm {*}\simeq 16m_\mathrm {H}\), \(p_\mathrm {*}=9\))...
4.La métallicité du Soleil varie selon les sources de \(Z_\odot =0.013\) à \(Z_\odot =0.018\) [1, 5].
5.Exception faite des naînes blanches et étoiles à neutrons où la matière est dégénérée voir cristallisée.
6.L’émission stimulée le long du chemin parcouru par les photons, proportionnelle par définition à \(L\), est incluse dans \(\kappa \) ; en l’absence du terme source \(j\), la relation de bilan détaillé \eqref{eq:bilandetaille} n’a pas de solution physique et l’équilibre thermodynamique ne peut être atteint. La thermodynamique démontre ansi l’existence d’une émission spontanée que seule une quantification appropriée des champs révèle en mécanique quantique.
7.Il s’agit stricto-sensu de la température des photons, laquelle est supposée égale à celle de la matière en vertu des hypothèses d’équilibre local et des échanges entre eux décrits par \(j_\nu \) et \(\kappa _\nu \). En particulier, si \(\kappa _\nu \approx 0\), les photons émis par le coeur traversent l’étoile sans interagir avec la matière. La « température » des photons (celle du coeur, si tant est qu’on puisse assimiler son rayonnement à celui d’un corps noir) se découple alors de celle de la matière. L’étoile n’apparaît alors plus comme un système de matière et de photons à l’équilibre qui rayonne comme un corps noir à sa température de surface, et les hypothèses d’équilibre local faites jusqu’ici ne sont plus valables. De façon générale, l’établissement d’un équilibre local suppose que le libre parcours moyen \(\ell \) des photons reste petit devant les longueurs caractéristiques de variation de la température \(\approx T/(dT/dr)\).
8.Ce n’est plus strictement vrai cependant si les degrés de liberté internes sont fortement anharmoniques, et/ou si les énergies de quantification associées sont comparables à \(kT\).
9.Pour exemple, un gaz parfait diatomique tel que O\(_2\) possède 5 degrés de liberté harmoniques par molécule (voir chapitre 1), et a donc une énergie interne \(\varepsilon =\tfrac {5}{2}kT\) par particule alors que sa pression reste \(P=nkT\) ; par conséquent \(c_\mathrm {v}=\frac {5}{2}k\) par particule, \(c_\mathrm {p}=c_\mathrm {v}+k=\frac {7}{2}k\) par particule, et \(\gamma =7/5\).
10.On néglige ici la pression de radiation.
11.Plus précisément, on peut définir la surface de base \(r=r_\mathrm {p}\) de la photosphère comme le lieu où la profondeur optique \(\log [I(r_0)/I(r_\mathrm {p})]\) vaut 1, avec \(I(r)\) l’intensité énergétique d’un faisceau de longueur d’onde \(\lambda \simeq 500\) nm émis depuis \(r=r_0\gg r_\mathrm {p}\), et ayant traversé l’atmosphère du Soleil sous incidence normale.
12.La température n’y décroît pas de façon monotone, la couronne solaire pouvant atteindre 2 000 000 K.
13.On a également \(P(r)\rho (r)^{-\gamma }=\mathrm {Constante}\) : La zone de convection est un polytrope d’indice \(\gamma =5/3\).
14.Sa composition devrait donc être plus homogène.
15.On peut d’ailleurs le vérifier sur les simulations des figures 2.7 et 2.8 : \(L(10M_\odot )/L(M_\odot )=10^{3.73}\).
16.Et on peut encore le vérifier sur les simulations des figures 2.7 et 2.8 : \(R(10M_\odot )/R(M_\odot )=10^{0.51}\) et \(T_\mathrm {c}(10M_\odot )/T_\mathrm {c}(M_\odot )=10^{0.68}\).