Ce chapitre introduit les notions fondamentales permettant de décrire une étoile dans l’approximation la plus simple d’équilibre hydrostatique et thermodynamique local. Cette étoile sera modélisée comme un gaz (plasma) d’électrons et de noyaux soumis à sa propre pesanteur (qui tend à l’effondrer), et à une pression de matière et de rayonnement entretenue par les réactions thermonucléaires en son coeur (qui s’oppose à cet effondrement). Le paragraphe 1.2 démontre donc les équations d’état d’un « gaz parfait » de fermions et ses limites classique et dégénérée. Le paragraphe 1.3 décrit ensuite les photons, le rayonnement du corps noir et la pression de radiation. Le paragraphe 1.4 rappelle quelques éléments sur les forces de pesanteur qui s’exercent sur l’étoile et établit les conditions d’équilibre d’une structure auto-gravitante. Enfin, le paragraphe 1.5 introduit la fusion nucléaire et la nucléosynthèse dans les étoiles. Le modèle hydrostatique de l’étoile lui-même sera décliné au chapitre 2.
On considère un gaz de fermions (électrons ou noyaux...) soumis à des interactions permettant de maintenir ce gaz à l’équilibre avec un réservoir à température \(T\) et potentiel chimique \(\mu \) (ensemble grand-canonique), mais néanmoins négligeables devant leur énergie cinétique (gaz « parfait »). L’Hamiltonien de chaque particule de masse \(m\) est donc :
\begin {equation} H=\frac {1}{2m}\vec {p}^2=\frac {1}{2m}\left (p_x^2+p_y^2+p_z^2\right ), \label {eq:Hamiltonien} \end {equation}
où \(\vec {p}=-i\hbar \boldsymbol {\nabla }\) est l’opérateur impulsion et \(p_x\), \(p_y\), \(p_z\) ses composantes cartésiennes. Les états propres de cet Hamiltonien sont les ondes planes \(\psi _\vec {k}(\vec {r})=e^{i\vec {k}\cdot \vec {r}}/\sqrt {V}\) qui ont pour énergie
\begin {equation} E_\vec {k}=\frac {\hbar ^2\vec {k}^2}{2m}=\frac {1}{2}m\vec {v}_\vec {k}^2 \label {eq:Ek} \end {equation}
et pour vitesse \(\vec {v}_\vec {k}=\hbar \vec {k}/m\). A la limite thermodynamique1, on peut en toute généralité assimiler le volume \(V\) occupé par le gaz à un parallélépipède de cotés \(L_x\times L_y\times L_z\), auquel on applique des conditions aux limites périodiques ; le vecteur d’onde \(\vec {k}\) est donc quantifié :
\begin {equation} k_x=\frac {2\pi }{L_x}n_x\,;\,k_y=\frac {2\pi }{L_y}n_y\,;\,k_z=\frac {2\pi }{L_z}n_z\,, \end {equation}
avec \(n_x\), \(n_y\), \(n_z\in \mathbb {Z}\). A l’équilibre, chaque état est (en moyenne) occupé par \(p_\vec {k}=n_s f(E_\vec {k})\) particules, où \(n_s\) la dégénérescence de spin des fermions (\(n_s=2\) pour des spins \(\tfrac {1}{2}\)), et
\begin {equation} f(\varepsilon )=\frac {1}{1+e^{\beta (\varepsilon -\mu )}} \end {equation}
est la distribution de Fermi-Dirac, avec \(\beta =1/(kT)\). On peut ainsi calculer la valeur moyenne d’ensemble de toute observable \(O\) :
\begin {equation} \langle O\rangle =n_s\sum _{n_x,n_y,n_z\in \mathbb {Z}} O_\vec {k}f(E_\vec {k})\approx V\int _{\mathbb {R}^3} d^3\vec {k}\,\rho _\vec {k}O_\vec {k}f(E_\vec {k})\,, \end {equation}
où \(O_\vec {k}=\langle \psi _\vec {k}|O|\psi _\vec {k}\rangle \) et \(\rho _\vec {k}=n_s/(2\pi )^3\) est la densité d’états par unité de volume (spin compris) dans l’espace réciproque. Si \(O_\vec {k}\) ne dépend (comme l’énergie) que de \(k=|\vec {k}|\),
\begin {equation} \langle O\rangle =4\pi V\int _0^\infty dk\,\rho _k k^2 O_k f(E_k)\,. \end {equation}
On effectue finalement le changement de variable \(k=\sqrt {2mE}/\hbar \) pour intégrer sur l’énergie plutôt que sur le vecteur d’onde :
\begin {equation} \langle O\rangle =V\int _0^\infty d\varepsilon \,\rho (\varepsilon )O(\varepsilon )f(\varepsilon )\,, \end {equation}
avec
\begin {equation} \rho (\varepsilon )=4\pi \rho _k k^2\frac {dk}{dE}=\frac {n_s}{(2\pi )^2}\left (\frac {2m}{\hbar ^2}\right )^{3/2}\sqrt {\varepsilon } \end {equation}
la densité d’états par unité de volume et d’énergie et \(O(\varepsilon )\equiv O_{k=\sqrt {2mE}/\hbar }\). L’énergie interne moyenne du gaz est donc [\(O(\varepsilon )=\varepsilon \)] :
\begin {equation} \langle E\rangle =V\int _0^\infty d\varepsilon \,\rho (\varepsilon )\varepsilon f(\varepsilon )=V\frac {n_s}{(2\pi )^2}\left (\frac {2m}{\hbar ^2}\right )^{3/2}\frac {3\sqrt {\pi }}{4}(kT)^{5/2}F_{3/2}(\beta \mu ) \label {eq:E} \end {equation}
tandis que le nombre moyen de particules dans le gaz est [\(O(\varepsilon )=1\)] :
\begin {equation} \langle N\rangle =V\int _0^\infty d\varepsilon \,\rho (\varepsilon )f(\varepsilon )=V\frac {n_s}{(2\pi )^2}\left (\frac {2m}{\hbar ^2}\right )^{3/2}\frac {\sqrt {\pi }}{2}(kT)^{3/2}F_{1/2}(\beta \mu ) \label {eq:N} \end {equation}
où \(F_\alpha \) est l’intégrale de Fermi :
\begin {equation} F_\alpha (x)=\frac {1}{\Gamma (\alpha +1)}\int _0^\infty dt\,\frac {t^\alpha }{1+e^{(t-x)}} \end {equation}
et \(\Gamma (\alpha )\) la fonction Gamma2 :
\begin {equation} \Gamma (\alpha +1)=\int _0^\infty dt\,t^\alpha e^{-t}\,. \end {equation}
A la limite thermodynamique, on peut assimiler \(\langle E\rangle \equiv E\) et \(\langle N\rangle \equiv N\) à des grandeurs déterministes et inverser \eqref{eq:N} pour calculer \(\mu \) que l’on substitue dans \eqref{eq:E} pour exprimer l’énergie interne en fonction de \(N\), \(V\) et \(T\). Les intégrales de Fermi ne sont toutefois pas analytiques en dehors des cas (heureusement pertinents!) suivants.


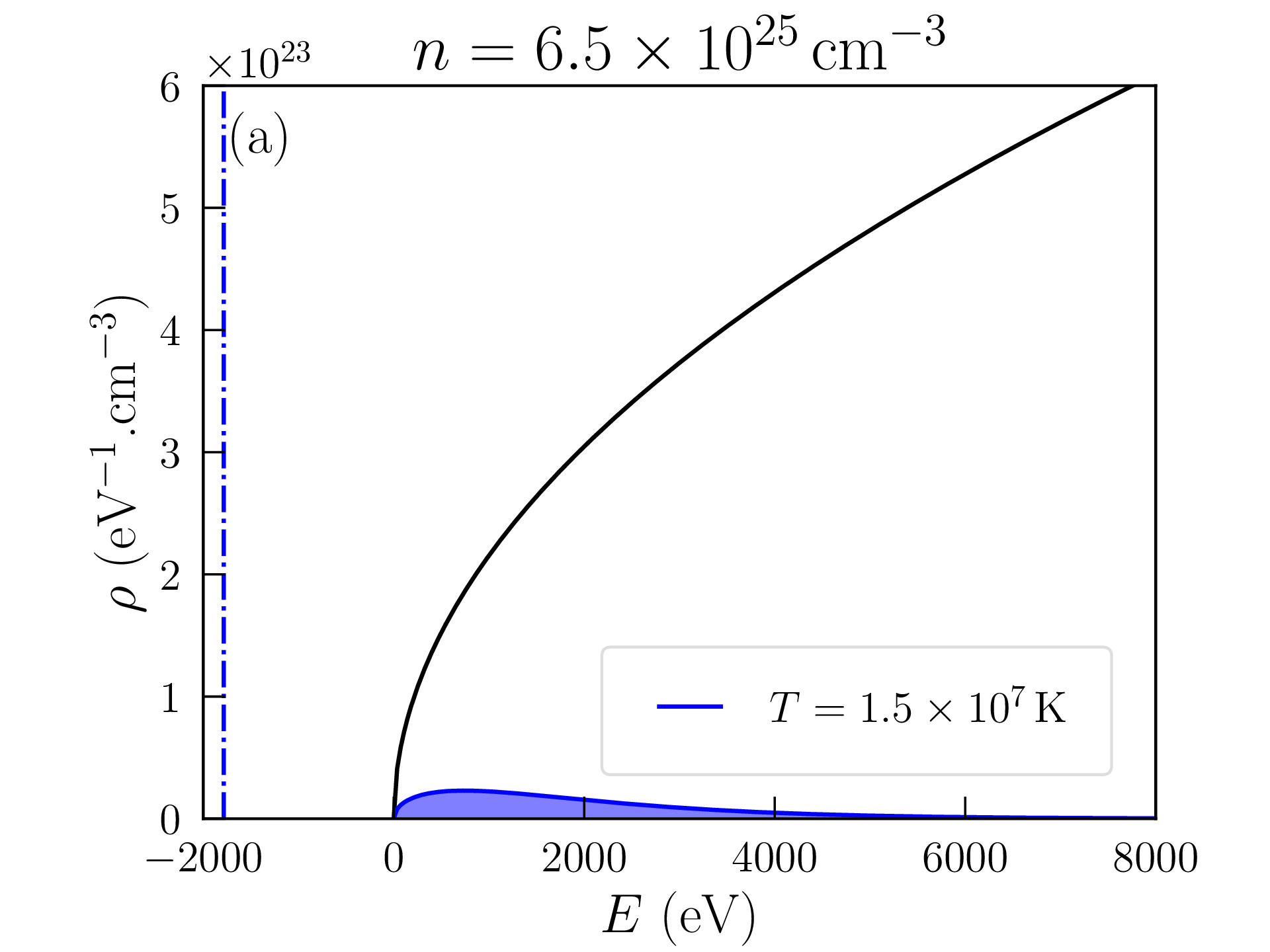
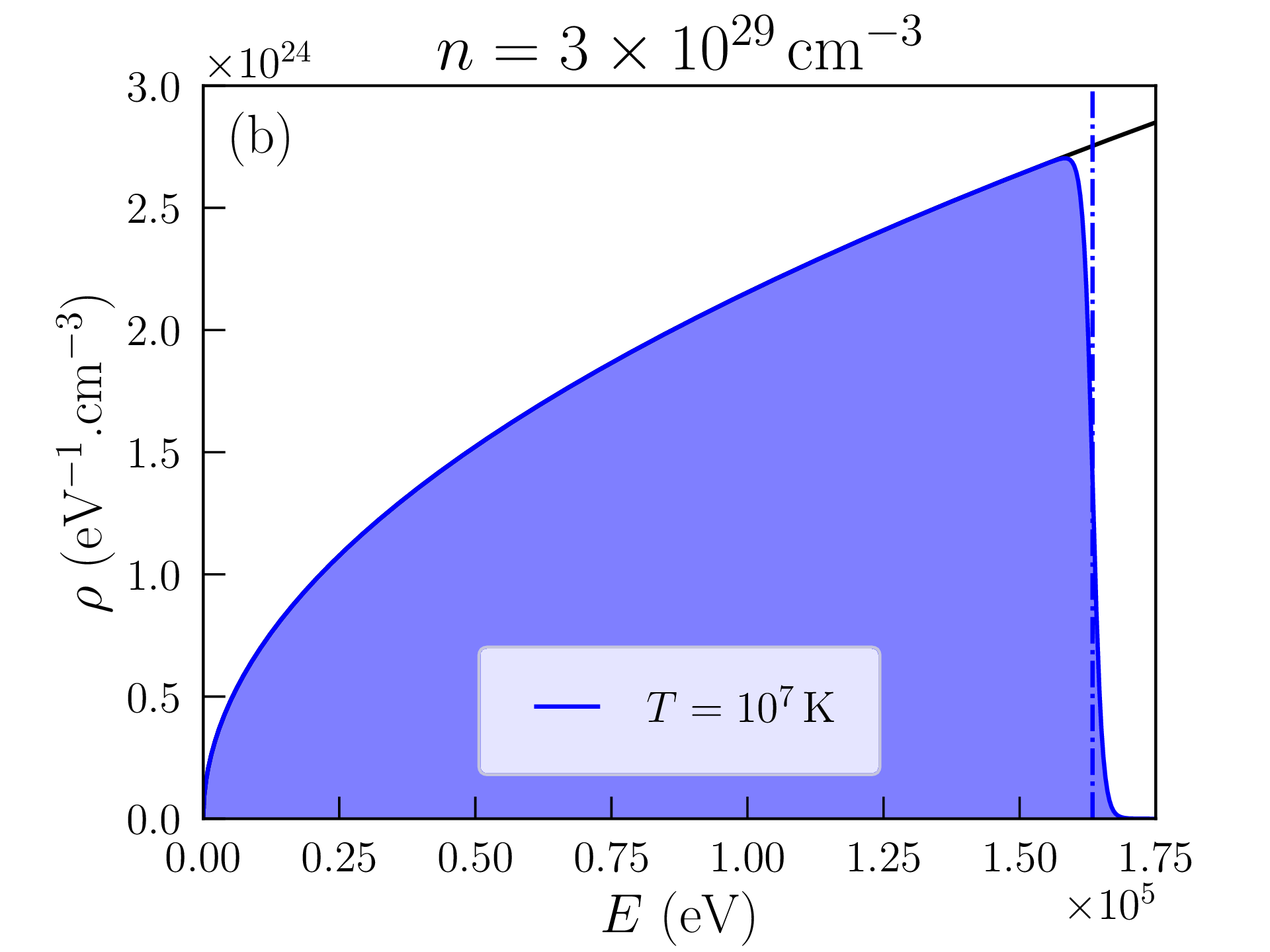
Si la densité \(n=N/V\) du gaz est suffisamment faible, et/ou la température \(T\) est suffisamment élevée, la distribution de Fermi-Dirac peut-être assimilée à une distribution de Maxwell-Boltzmann (\(\mu \ll -kT\), voir Fig. 1.1a) :
\begin {equation} f(\varepsilon )=\frac {1}{1+e^{\beta (\varepsilon -\mu )}}\approx e^{-\beta (\varepsilon -\mu )}\ \forall \varepsilon >0\,. \end {equation}
Le nombre moyen de particules par niveau d’énergie est ainsi \(p_\vec {k}\ll n_s\) de sorte que le principe d’exclusion de Pauli ne domine pas la physique du gaz. Les intégrales de Fermi se simplifient alors :
\begin {equation} F_\alpha (x)\approx e^x\frac {1}{\Gamma (\alpha +1)}\int _0^\infty dt\,t^\alpha e^{-t}=e^x\,. \end {equation}
Par conséquent,
\begin {align} N&=V\frac {n_s}{(2\pi )^2}\left (\frac {2m}{\hbar ^2}\right )^{3/2}\frac {\sqrt {\pi }}{2}(kT)^{3/2}e^{\beta \mu } \label {eq:Nclass} \\ E&=V\frac {n_s}{(2\pi )^2}\left (\frac {2m}{\hbar ^2}\right )^{3/2}\frac {3\sqrt {\pi }}{4}(kT)^{5/2}e^{\beta \mu } \,. \end {align}
En substituant la première relation dans la seconde, il vient :
On retrouve là le théorème d’équipartition de l’énergie : l’énergie interne d’un gaz classique à température \(T\) est égale à \(\tfrac {1}{2}kT\) par degré de liberté quadratique dans l’Hamiltonien (ici, les impulsions \(p_x\), \(p_y\), \(p_z\) des \(N\) particules). L’énergie interne par particule est donc :
\begin {equation} \varepsilon =\frac {E}{N}=\frac {3}{2}kT\,. \label {eq:Eclass1} \end {equation}
La pression du gaz peut ensuite être définie à partir de considérations cinétiques ou thermodynamiques (dérivée isentropique de l’énergie interne par rapport au volume).
A cet effet, imaginons une paroi de surface \(S=L_yL_z\) perpendiculaire à \(x\), avec le gaz à sa gauche (la position et la direction choisie n’ont aucune importance dans un gaz homogène et isotrope). La force à excercer sur cette paroi pour la maintenir en place est l’opposée de la quantité de mouvement que lui transfère le gaz par unité de temps :
\begin {equation} \vec {F}=-\frac {d}{dt}\langle \vec {p}_t\rangle \,. \end {equation}
Durant un intervalle de temps \(dt\), seules les particules ayant une vitesse \(v_x=\hbar k_x/m>0\) se trouvant dans un volume \(dV=Sv_xdt\) vont rebondir3 sur la paroi et lui transférer une quantité de mouvement élémentaire \(\delta p_x=2p_x=2mv_x=2\hbar k_x\). Par conséquent, la quantité de mouvement totale transférée à la paroi est :
\begin {equation} dp_x=\int _{k_x>0}d^3\vec {k}\,\rho _\vec {k}(Sv_xdt)(2p_x)f(E_\vec {k})\,, \end {equation}
La pression exercée par le gaz sur la paroi est la force \(-F_x=dp_x/dt\) par unité de surface :
\begin {equation} P=2\int _{k_x>0}d^3\vec {k}\,\rho _\vec {k}v_xp_xf(E_\vec {k})=\int _{\mathbb {R}^3}d^3\vec {k}\,\rho _\vec {k}v_xp_xf(E_\vec {k})\,. \label {eq:Pcinetique} \end {equation}
Soit encore :
\begin {equation} P=\int _{\mathbb {R}^3}d^3\vec {k}\,\rho _\vec {k}mv_x^2f(E_\vec {k})=nm\langle v_x^2\rangle \,, \end {equation}
où \(\langle v_x^2\rangle \) est la vitesse carrée moyenne par particule (mesurée le long de \(x\)). Dans un gaz isotrope, \(\langle v_x^2\rangle =\langle v_y^2\rangle =\langle v_z^2\rangle =\langle \vec {v}^2\rangle /3\), si bien que :
\begin {equation} P=\frac {1}{3}nm\langle \vec {v}^2\rangle \,. \end {equation}
Enfin, l’Hamiltonian du gaz étant purement cinétique, l’énergie interne par particule est :
\begin {equation} \varepsilon =\frac {1}{2}m\langle \vec {v}^2\rangle \,, \end {equation}
de sorte que :
\begin {equation} P=\frac {2}{3}n\varepsilon =\frac {2}{3}\eta \,, \label {eq:Pcin} \end {equation}
où \(\eta =n\varepsilon =E/V\) est la densité d’énergie interne. En substituant \eqref{eq:Eclass1} dans \eqref{eq:Pcin}, on obtient finalement « l’équation d’état des gaz parfaits » :
Alternativement, la pression définit la quantité de travail \(dW=-PdV\) à fournir pour faire varier le volume \(V\) du gaz ; \(dE=dW\) est donc la variation d’énergie interne \(E\) du gaz lors d’une compression/dilatation adiabatique (i.e., à entropie \(S\) et nombre de particules \(N\) constants) :
\begin {equation} P=-\left (\frac {\partial E}{\partial V}\right )_{S,N}\,. \end {equation}
A la limite thermodynamique, on peut par commodité utiliser la définition micro-canonique de l’entropie :
\begin {equation} S=k\log \Omega (E)\,, \end {equation}
où \(\Omega (E)\) est le nombre d’états accessibles aux particules dans le gaz d’énergie interne \(E\). Comme
\begin {equation} E=\frac {\hbar ^2}{2m}\sum _{i=1}^N\sum _{\alpha \in \{x,y,z\}} k_{i\alpha }^2\,, \end {equation}
les surfaces d’énergie constantes sont des hyper-sphères de rayon \(k(E)=\sqrt {2mE}/\hbar \) dans l’espace \(\mathbb {R}^{3N}\) des \(N\) vecteurs d’ondes \(\vec {k}_i\). Le nombre d’états à l’intérieur de l’hyper-sphère de rayon \(k(E)\) est :
\begin {equation} {\cal N}(E)=\frac {1}{N!}\rho _\vec {k}^N{\cal V}(E) \label {eq:NHS} \end {equation}
où :
\begin {equation} {\cal V}(E)=\frac {\pi ^{3N/2}}{\Gamma (3N/2+1)}k(E)^{3N} \end {equation}
est le volume de cette hyper-sphère. Le facteur \(N!\) au dénominateur de \eqref{eq:NHS} rend compte du fait que tous les états obtenus par simple permutation des \(N\) particules sont indiscernables. On approxime ensuite \(\Omega (E)\) comme le nombre d’états entre les hyper-sphères de rayons \(E\) et \(E+\delta E\) :
\begin {equation} \Omega (E)={\cal N}(E+\delta E)-{\cal N}(E)\,, \end {equation}
soit :
\begin {equation} \Omega (E)\sim \frac {d{\cal N}(E)}{dE}\delta E=\frac {3N}{2N!\Gamma (3N/2+1)}\left [n_s V\left (\frac {2\pi mE}{h^2}\right )^{3/2}\right ]^{N}\frac {\delta E}{E}\,. \end {equation}
Le choix de \(\delta E\) est sans importance à la limite thermodynamique \(N\to \infty \) car il ne donne pas lieu à des contributions extensives (\(\propto N\)) à l’entropie. En utilisant \(\Gamma (3N/2+1)\equiv (3N/2)!\) et la formule asymptotique de Stirling \(N!\sim (N/e)^N\sqrt {2\pi N}\), on obtient en effet :
\begin {equation} \Omega (E)\sim Ce^{5N/2}\left [n_s\frac {V}{N}\left (\frac {4\pi m}{3h^2}\right )^{3/2}\left (\frac {E}{N}\right )^{3/2}\right ]^{N}\frac {\delta E}{E}\,, \end {equation}
où \(C\) est une constante numérique. L’entropie par particule \(s=S/N\) est donc à la limite thermodynamique :
\begin {equation} s=k\log \left [\frac {n_s}{n}\left (\frac {4\pi m\varepsilon }{3h^2}\right )^{3/2}\right ]+\frac {5}{2}k\,. \end {equation}
Lors d’une variation adiabatique de volume,
\begin {equation} ds=0\Rightarrow d(VE^{3/2})=0\Rightarrow dVE^{3/2}+\frac {3}{2}VE^{1/2}dE=0\,, \end {equation}
et donc :
\begin {equation} P=-\left (\frac {\partial E}{\partial V}\right )_{S,N}=\frac {2}{3}\frac {E}{V}=\frac {2}{3}\eta \,. \end {equation}
On retrouve là le résultat \eqref{eq:Pcin} de la théorie cinétique. Au cours d’une telle transformation adiabatique, on a en outre \(VE^{3/2}\propto V^{5/2}P^{3/2}\) constant, soit équivalemment
\begin {equation} PV^\gamma ,\ TV^{\gamma -1}\text {\ et\ }T^\gamma P^{1-\gamma }\text {\ constants}, \label {eq:Laplace} \end {equation}
avec \(\gamma =5/3\) le coefficient adiabatique du gaz (loi de Laplace).
Il convient de remarquer que l’énergie interne \eqref{eq:Eclass} et la pression \eqref{eq:Pcin} d’un gaz parfait classique sont strictement proportionnels à sa température. En effet, lorsque \(T\to 0\), toutes les particules occupent le niveau fondamental \(\psi _{\vec {k}=\vec {0}}\) d’énergie \(E=0\) et d’impulsion nulle. Cependant, le principe d’exclusion de Pauli, qui interdit à chaque niveau d’accueillir plus de \(n_s\) particules, ne permet pas une telle condensation ; le gaz va « dégénérer » bien avant.
Dans la limite inverse \(\mu \gg kT\) (température basse au regard de la densité), le gaz est dit dégénéré : une fraction significative des niveaux d’énergie sont occupés par le nombre maximal \(n_s\) de particules permis par le principe d’exclusion de Pauli (voir Fig. 1.1b). On a alors à l’ordre 0 en température :
\begin {equation} f(\varepsilon )=1\text { si }\varepsilon \le \mu \text { et }0\text { sinon.} \end {equation}
On peut dès lors intégrer analytiquement l’énergie interne et le nombre de particules :
\begin {align} N&=\int _0^\mu d\varepsilon \,\rho (\varepsilon )f(\varepsilon )=V\frac {n_s}{(2\pi )^2}\left (\frac {2m}{\hbar ^2}\right )^{3/2}\left (\frac {2}{3}\mu ^{3/2}\right ) \\ E&=\int _0^\mu d\varepsilon \,\rho (\varepsilon )\varepsilon f(\varepsilon )=V\frac {n_s}{(2\pi )^2}\left (\frac {2m}{\hbar ^2}\right )^{3/2}\left (\frac {2}{5}\mu ^{5/2}\right )\,. \end {align}
On calcule ensuite le potentiel chimique (énergie du dernier état occupé) à partir de la première équation :
\begin {equation} \mu =\frac {\hbar ^2}{2m}\left (6\pi ^2\frac {n}{n_s}\right )^{2/3}\,. \label {eq:mudeg} \end {equation}
En substituant \(\mu \) dans la seconde équation, on exprime enfin l’énergie interne \(E\) du gaz en fonction de \(N\), \(V\) (et \(T\ll \mu /k\)) :
\begin {equation} E=\frac {3}{5}N\mu =\frac {3\hbar ^2}{10m}\left (\frac {6\pi ^2}{n_s}\right )^{2/3}n^{5/3}V\,, \label {eq:Edeg} \end {equation}
soit par particule :
\begin {equation} \varepsilon =\frac {E}{N}=\frac {3}{5}\mu =\frac {3\hbar ^2}{10m}\left (6\pi ^2\frac {n}{n_s}\right )^{2/3}\,. \label {eq:Edeg1} \end {equation}
L’équation \eqref{eq:Pcinetique} est également valable dans un gaz dégénéré. Par conséquent, la pression cinétique est, comme dans le gaz classique4,
\begin {equation} P=\frac {2}{3}\eta =\frac {2}{3}\frac {E}{V}\,, \end {equation}
c’est à dire :
\begin {equation} P=\frac {\hbar ^2}{5m}\left (\frac {6\pi ^2}{n_s}\right )^{2/3}n^{5/3}\,. \label {eq:Pdeg} \end {equation}
Contrairement à un gaz classique, un gaz de fermions dégénéré exerce une pression finie à température \(T\to 0\) (parce que les particules remplissent tous les niveaux d’énergie jusqu’au potentiel chimique \(\mu \) à cause du principe d’exclusion de Pauli). Cette pression résiduelle s’appelle la pression de dégénérescence. Elle joue un rôle fondamental dans la physique des étoiles très évoluées (équilibre hydrostatique des naînes blanches, ...).
La condition de dégénérescence peut s’écrire \(\mu \approx 0\) ; en injectant cette condition dans \eqref{eq:Nclass}, on obtient la densité critique
\begin {equation} n_\mathrm {deg}\approx n_s\left (\frac {mkT}{2\pi \hbar ^2}\right )^{3/2} \label {eq:ndeg} \end {equation}
au delà de laquelle le gaz dégénère à température \(T\) fixée. Cette densité critique croît comme \(T^{3/2}\) car l’énergie cinétique du gaz augmente avec la température et sa fonction de distribution s’étale. En assimilant le volume occupé par chaque particule à un cube de côté \(\Lambda =n^{-1/3}\), on peut calculer la distance moyenne entre celles-ci lorsque le gaz dégénére :
\begin {equation} \Lambda _\mathrm {deg}=n_\mathrm {deg}^{-1/3}\approx n_s^{-1/3}\hbar \sqrt {\frac {2\pi }{mkT}}\,. \label {eq:ldeg} \end {equation}
Cette distance est connue sous le nom de longueur thermique de de Broglie (éventuellement au facteur \(n_s^{-1/3}\) près)5. A densité constante, le gaz dégénère en dessous de la température :
\begin {equation} T_\mathrm {deg}=\frac {2\pi \hbar ^2}{mk}\left (\frac {n}{n_s}\right )^{2/3}\,. \label {eq:Tdeg} \end {equation}
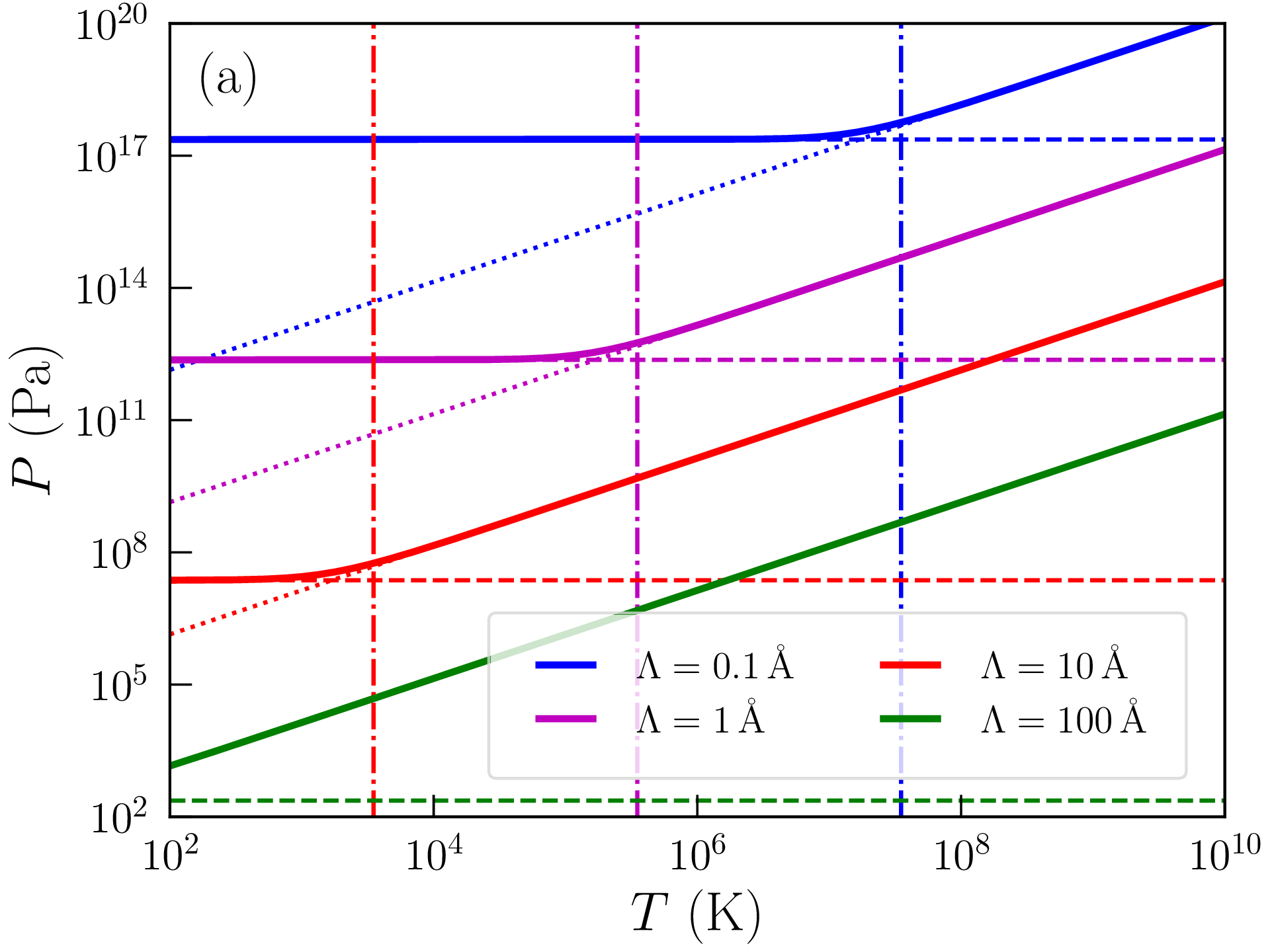
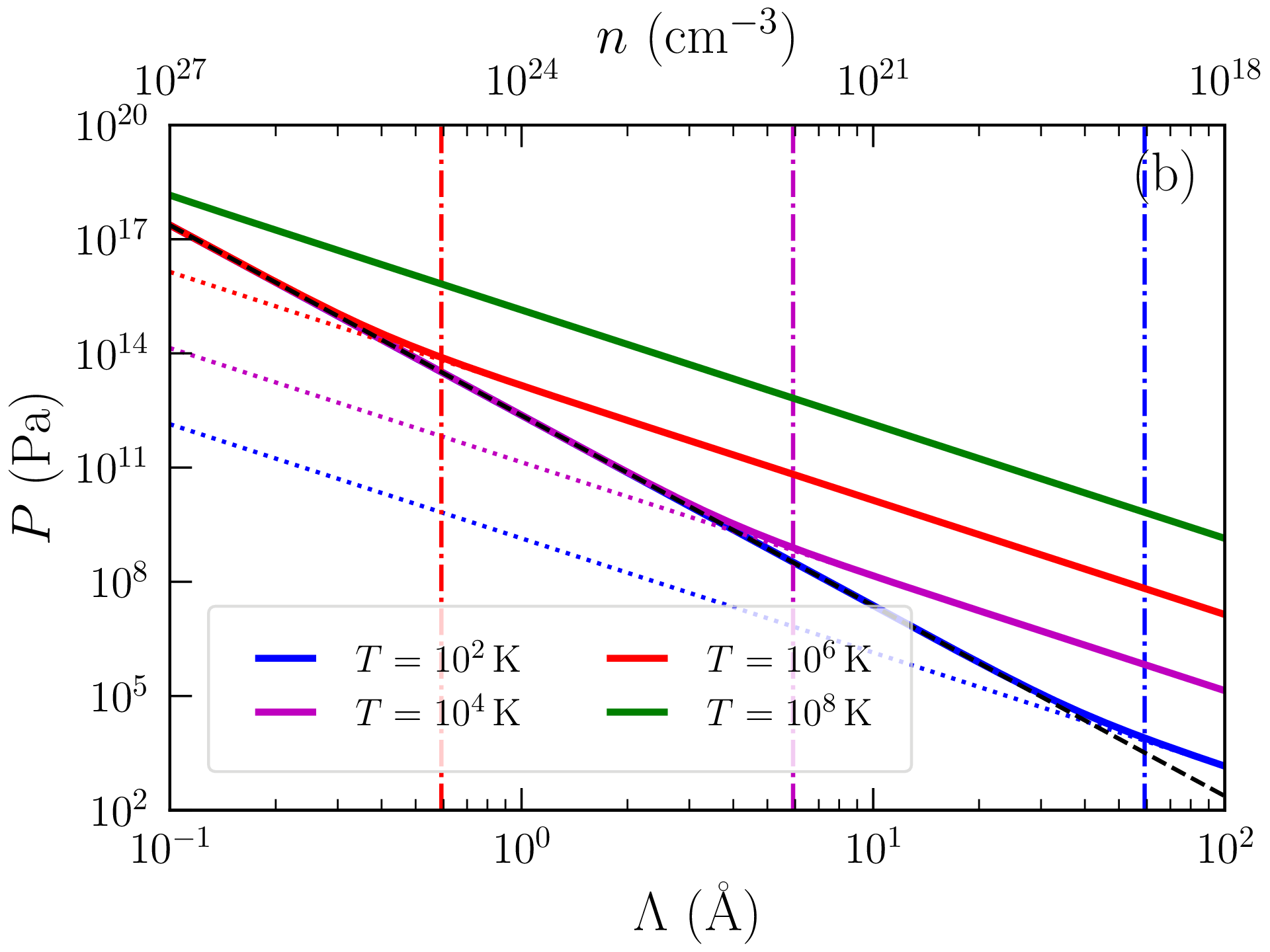
On peut résoudre numériquement les équations \eqref{eq:E} et \eqref{eq:N} pour calculer l’energie interne par particule \(\varepsilon \) et la pression \(P=\tfrac {2}{3}n\varepsilon \) d’un gaz de fermions de densité arbitraire \(n\) maintenu à température \(T\) (voir le code idealfermiongas.py). La figure 1.2(a) représente ainsi la pression \(P\) dans un gaz d’électrons (\(m=9.1\times 10^{-31}\)kg, \(n_s=2\)) en fonction de la température \(T\) à distance moyenne entre particules \(\Lambda =n^{-1/3}\) constante. La figure 1.2(b) représente de même la pression \(P\) en fonction de \(\Lambda \) à température \(T\) constante. Les différents régimes (classique, dégénéré) sont facilement identifiables et les transitions coincident avec les densités \(n_\mathrm {deg}\) et températures \(T_\mathrm {deg}\) reportées sur ces figures. On remarquera en particulier que la pression est quasiment indépendante de la température dans un gaz dégénéré6.
Les particules du gaz peuvent présenter des degrés de liberté internes qui contribuent à son énergie totale. Par exemple, un gaz parfait d’une molécule diatomique telle que O\(_2\) possède cinq degrés de liberté par particule à basse énergie (les trois translations du centre de gravité et les deux rotations d’ensemble de la molécule) ; en supposant ces degrès de libertés faiblement quantifiés (variables classiques continues) et harmoniques, on a alors d’après le théorème d’équipartition de l’énergie \(\varepsilon =\frac {5}{2}kT\) par molécule. A plus haute énergie (donc à plus haute température), on pourra aussi sonder le spectre vibrationnel de la molécule (le degré de liberté restant), qui est lui fortement quantifié et ne satisfait donc pas aux conditions du théorème d’équipartition. Toutefois, la théorie cinétique suggère (en première approximation) que seule importe l’impulsion du centre de masse pour définir la pression, et par conséquent que l’équation d’état \(P=nkT\) reste valable pour un tel gaz. Il en va de même pour un gaz de noyaux atomiques, qui possèdent des degrés de liberté rotationnels et vibrationnels (à relativement haute énergie cependant).
Les gaz peuvent être des mélanges de particules discernables (électrons, noyaux de différents types...). De façon générale, l’énergie interne et la pression totale sont la somme des énergies et pressions partielles de chaque type \(\nu \) de particule, caractérisés par leurs densités respectives \(n_\nu \), masse \(m_\nu \), et dégénerescence de spin \(n_{s\nu }\). Dans le cas classique, non dégénéré, la pression ne dépend que de la densité totale de particules \(n=\sum _\nu n_\nu \) :
\begin {equation} P=nkT\,. \end {equation}
Si une ou plusieurs composantes du gaz sont dégénérées, il faut utiliser \eqref{eq:Pdeg} avec les \(n_\nu \), \(m_\nu \), et \(n_{s\nu }\) correspondants. La densité de dégénérescence \(n_\mathrm {deg}\) étant proportionnelle à \(m^{3/2}\) [Eq. \eqref{eq:ndeg}], les électrons dégénèrent en particulier bien avant les noyaux dans un plasma.
En pratique, les particules du gaz peuvent entretenir des interactions à longue portée, en particulier si elles sont chargées (ce qui est le cas dans les plasmas rencontrés dans les étoiles). Ces interactions peuvent dominer la physique du gaz dans certains régimes et changer radicalement sa structure et son équation d’état (formation des atomes et molécules, cristallisation de Wigner dans les gaz d’électrons, ...). Une simple analyse dimensionnelle suggère que l’énergie cinétique du gaz est \(\propto \Lambda ^{-2}\) alors que son énergie Coulombienne (interactions de paires en \(1/r\) dans un système globalement neutre) est \(\propto \Lambda ^{-1}\) (cf. modèle du jellium). Par conséquent, l’énergie cinétique domine la physique du gaz à haute densité et/ou haute température, alors que les interactions Coulombiennes prennent le pas à basse densité et basse température. Dans les conditions chaudes et/ou denses recontrées dans les étoiles, elles ne jouent donc pas de rôle majeur, mais peuvent néanmoins donner lieu à quelques corrections quantitatives.
Il convient en principe de vérifier que le gaz n’est pas devenu relativiste (auquel cas il faut substituer l’équation de Dirac à \eqref{eq:Hamiltonien}), et donc que :
\begin {equation} \varepsilon =\frac {1}{2}m\langle \vec {v}^2\rangle \ll \frac {1}{2}mc^2\,, \end {equation}
où \(c=299\,792\,458\)m/s est la vitesse de la lumière dans le vide. Dans un gaz non dégénéré, où \(\varepsilon =\tfrac {3}{2}kT\), la température doit par conséquent rester bien inférieure à :
\begin {equation} T_\mathrm {r}=\frac {mc^2}{3k} \end {equation}
qui vaut \(T_\mathrm {r}\approx 2\times 10^{9}\)K pour des électrons. Dans un gaz dégénéré, on obtient plutôt de \eqref{eq:Edeg1} une relation sur la densité :
\begin {equation} n\ll n_\mathrm {r}=\frac {n_s}{6\pi ^2}\left (\sqrt {\frac {5}{3}}\frac {mc}{\hbar }\right )^3 \label {eq:nr} \end {equation}
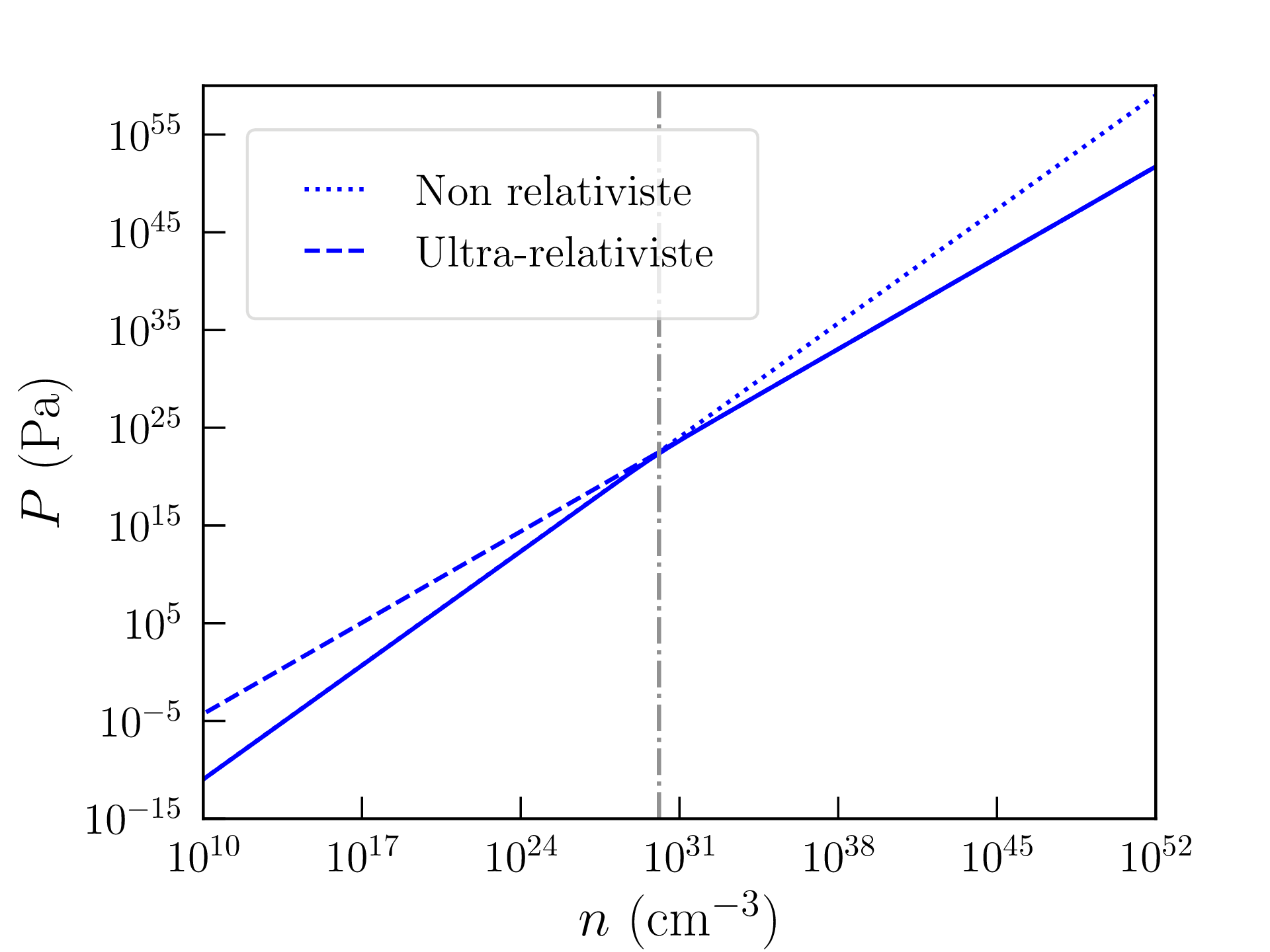
qui vaut \(n_\mathrm {r}\approx 1.25\times 10^{30}\)cm\(^{-3}\) pour des électrons. Les corrections relativistes sont donc déjà non négligeables (voir essentielles) dans certaines parties de la figure 1.2.
On peut établir l’équation d’état d’un gaz parfait au caractère arbitrairement relativiste en substituant à \eqref{eq:Ek} la relation de dispersion
\begin {equation} E_\vec {k}=\sqrt {m^2c^4+\vec {p}^2c^2}=\sqrt {m^2c^4+\hbar ^2\vec {k}^2c^2}\,. \end {equation}
L’impulsion (ou quantité de mouvement) des particules est \(\vec {p}=\hbar \vec {k}=\gamma m\vec {v}\), avec \(\vec {v}\) la vitesse et \(\gamma \) le facteur de Lorentz :
\begin {equation} \gamma =\frac {1}{\sqrt {1-\frac {\vec {v}^2}{c^2}}}\,. \end {equation}
En inversant cette relation il vient :
\begin {equation} \vec {v}=\frac {\hbar \vec {k}}{m}\frac {1}{\sqrt {1+\frac {\hbar ^2\vec {k}^2}{m^2c^2}}}=\frac {1}{\hbar }\boldsymbol {\nabla }_\vec {k}E_\vec {k}\,. \end {equation}
Lorsque \(\hbar ^2\vec {k}^2\ll m^2c^2\), \(\gamma \to 1\) et on retrouve :
\begin {equation} E_\vec {k}\simeq mc^2+\frac {\hbar ^2\vec {k}^2}{2m}\,, \end {equation}
où le premier terme est l’énergie de masse au repos et le second l’énergie cinétique non-relativiste \eqref{eq:Ek}. On peut aisément s’affranchir de l’énergie de masse au repos dans un gaz non relativiste en redéfinissant l’origine des énergies.
On peut démontrer que l’équation d’état \(P=nkT\) est toujours valable dans un gaz relativisite non dégénéré. On s’intéresse plus particulièrement ici à la limite dégénérée \(T\to 0\). Comme \(E_\vec {k}\) est une fonction croissante de \(k=|\vec {k}|\), les fermions occupent tous les états de vecteur d’onde \(k<k_\mathrm {F}\) tel que :
\begin {equation} n=\rho _\vec {k}\frac {4\pi }{3}k_\mathrm {F}^3\Rightarrow k_\mathrm {F}=\left (6\pi ^2\frac {n}{n_s}\right )^{1/3}\,. \end {equation}
Ce résultat est indépendant du caractère relativiste du gaz. La pression cinétique reste définie par \eqref{eq:Pcinetique} :
\begin {align} P&=\int _{\mathbb {R}^3}d^3\vec {k}\,\rho _\vec {k}v_xp_xf(E_\vec {k})=\int _{k<k_\mathrm {F}}d^3\vec {k}\,\rho _\vec {k}v_xp_x \nonumber \\ &=\frac {n_s}{(8\pi )^3}\int _0^{2\pi }d\varphi \int _0^{\pi } d\theta \,\sin \theta \int _0^{k_\mathrm {F}}dk\,k^2\hbar k\cos \theta \frac {\frac {\hbar k}{m}\cos \theta }{\sqrt {1+\frac {\hbar ^2\vec {k}^2}{m^2c^2}}} \nonumber \\ &=\frac {n_sm^4c^5}{6\pi ^2\hbar ^3}F\left (\frac {\hbar k_\mathrm {F}}{mc}\right )\,, \label {eq:Pdegrel} \end {align}
où :
\begin {equation} F(x)=\int _0^x du\,\frac {u^4}{\sqrt {1+u^2}}\,. \end {equation}
La pression est représentée en fonction de la densité d’électrons \(n\) sur la figure 1.3. Dans la limite \(x=\hbar k_\mathrm {F}/(mc)\ll 1\), \(F(x)\sim x^5/5\) et on retrouve l’expression \eqref{eq:Pdeg} pour un gaz dégénéré non-relativiste (\(P\propto n^{5/3}\)). A l’inverse, dans la limite « ultra-relativiste » \(x=\hbar k_\mathrm {F}/(mc)\gg 1\), \(F(x)\sim x^4/4\) si bien que :
\begin {equation} P=\frac {\hbar c}{4}\left (\frac {6\pi ^2}{n_s}\right )^{1/3}n^{4/3}\,. \label {eq:Pdegurel} \end {equation}
La pression dans un gaz dégénéré ultra-relativiste croît donc comme \(n^{4/3}\) au lieu de \(n^{5/3}\) car les particules vont moins vite à quantité de mouvement égale. Cette « faible » dépendence à la densité implique l’existence d’une masse limite pour un objet dégénéré au-delà de laquelle il s’effondre sous son propre poids (masse de Chandrasekhar, voir paragraphe 1.4.4).
On peut de même calculer l’énergie et la pression d’un « gaz de photons » dans une enceinte7 à la température \(T\). Les photons sont des bosons sans masse ; les modes propres de photons dans le vide sont également des ondes planes caractérisées par leur vecteur d’onde \(\vec {k}\). Leur énergie \(E_\vec {k}=\hbar c|\vec {k}|\) est linéaire en \(k\), à la différence des particules massives, et leur impulsion est \(\vec {p}_\vec {k}=\hbar \vec {k}\) (comme pour ces dernières). La vitesse des photons dans le vide est \(\vec {v}_\vec {k}=c\vec {k}/k\) (\(|\vec {v}_\vec {k}|=c\)). On peut introduire la longueur d’onde \(\lambda =2\pi /k\) et la fréquence \(\nu =E/h\) et écrire indifféremment :
\begin {equation} E=h\nu =h\frac {c}{\lambda }=\hbar ck\,. \end {equation}
La dégénérescence des modes de photons est \(n_s=2\) (polarisations horaire et anti-horaire). On quantifie le vecteur d’onde comme au paragraphe 1.2 pour calculer les grandeurs thermodynamiques ; En équilibre à la température \(T\), chaque mode est en moyenne occupé par \(n_sf(E_\vec {k})\) photons où \(f\) est cette fois la fonction de distribution de Bose-Einstein :
\begin {equation} f(\varepsilon )=\frac {1}{e^{\beta \varepsilon }-1}\,. \label {eq:fbe} \end {equation}
On aura donc pour toute observable O telle que \(O_\vec {k}\) ne dépend que de \(k\) :
\begin {align} \langle O\rangle &=V\int _{\mathbb {R}^3} d^3\vec {k}\,\rho _\vec {k}O_\vec {k}f(E_\vec {k})=4\pi V\int _0^\infty dk\,\rho _k k^2 O_k f(E_k) \nonumber \\ &=V\int _0^\infty d\nu \,\rho (\nu )O(\nu )f(h\nu )\,, \end {align}
où \(k=2\pi \nu /c\) et \(\rho (\nu )\) est la densité d’états de photons par unité de volume et par unité de fréquence :
\begin {equation} \rho (\nu )=4\pi \rho _k k^2\frac {dk}{d\nu }=\frac {8\pi \nu ^2}{c^3}\,. \label {eq:rhoph} \end {equation}
En particulier, la densité d’énergie par unité de volume dans le gaz de photons est :
\begin {equation} \eta _\mathrm {r}=\int _0^\infty d\nu \,\rho (\nu )h\nu f(h\nu )\,. \end {equation}
En faisant le changement de variable \(x=\beta h\nu \),
\begin {equation} \eta _\mathrm {r}=\frac {8\pi (kT)^4}{(hc)^3}\int _0^\infty dx\,\frac {x^3}{e^x-1}=aT^4\,, \end {equation}
où8 :
\begin {equation} a=\frac {8\pi ^5k^4}{15h^3c^3}=7.566\times 10^{-16}\,\text {J/m$^3$/K$^4$} \end {equation}
est la constante de radiation.
Si des « parois » de l’enceinte sont transparentes, les photons vont fuir et le système va rayonner. Alternativement, si un objet est introduit dans l’enceinte, et atteint l’équilibre thermique avec le bain de photons, il doit rayonner autant de photons qu’il en reçoit (que ce soit par réflexion, absorption/émission, ... à chaque énergie et dans chaque direction). Ce rayonnement thermique est connu sous le nom de « rayonnement du corps noir9 » (parce que les objets froids ne rayonnent pas dans le visible). Dans le premier cas, le rayonnement émis correspond au flux de photons sortant de l’enceinte, et dans le second cas, au flux de photons rentrant dans le corps. Considérons donc une surface \(S\) perpendiculaire à \(x\) avec le gaz de photons à sa gauche (à nouveau, la position et l’orientation de cette surface n’ont aucune importance dans un système homogène et isotrope). La quantité d’énergie rayonnée au travers de cette surface pendant un intervalle de temps \(dt\) est :
\begin {equation} dE=\int _{k_x>0} d^3\vec {k}\,\rho _k\left (S\frac {k_x}{k}cdt\right )h\nu _kf(h\nu _k)\,. \end {equation}
La puissance rayonnée par unité de surface (densité de flux radiatif sortant ou excitance énergétique) est donc :
\begin {equation} M=\frac {1}{S}\frac {dE}{dt}=\int _{k_x>0} d^3\vec {k}\,\rho _k\left (\frac {k_x}{k}c\right )h\nu _kf(h\nu _k)\,, \end {equation}
qui s’intègre aisément en coordonnées sphériques (\(k_x=k\cos \theta \)) :
\begin {align} M&=\int _{0}^{2\pi }d\varphi \int _{0}^{\pi /2}d\theta \,\sin \theta \cos \theta \int _0^\infty dk\,\rho _k c k^2 h\nu _kf(h\nu _k) \nonumber \\ &=\int _{0}^{2\pi }d\varphi \int _{0}^{\pi /2}d\theta \,\sin \theta \cos \theta \int _0^\infty d\nu \,\frac {c}{4\pi }\rho (\nu )h\nu f(h\nu ) \nonumber \\ &=\int _{0}^{2\pi }d\varphi \int _{0}^{\pi /2}d\theta \,\sin \theta \cos \theta \int _0^\infty d\nu \,L_{\Omega ,\nu }(\nu )\,, \label {eq:Mcorpsnoir} \end {align}
où :
\begin {equation} L_{\Omega ,\nu }(\nu )=\frac {c}{4\pi }\rho (\nu )h\nu f(h\nu ) \label {eq:lep} \end {equation}
est la luminance énergétique spectrale. C’est la puissance émise à la fréquence \(\nu \) dans la direction \((\theta ,\varphi )\), par unité de fréquence, de surface effective du corps noir, et d’angle solide. Cette surface effective est la surface apparente \(S\cos \theta \) sous laquelle on voit \(S\) depuis un angle \(\theta \) avec sa normale (d’où le \(\cos \theta \) qui multiplie l’angle solide élémentaire \(d\Omega =\sin \theta d\theta d\varphi \)). Pour un corps en équilibre à la température \(T\),
\begin {equation} L_{\Omega ,\nu }(\nu ,T)=\frac {2h\nu ^3}{c^2}\frac {1}{e^{\beta h\nu }-1}\text {\ (loi de Planck).} \label {eq:planck} \end {equation}
On peut aisément terminer l’intégration dans l’hémisphère où rayonne \(S\) et écrire :
\begin {align} M=\int _0^\infty d\nu \,M_\nu (\nu )\,, \end {align}
où \(M_\nu (\nu )=\pi L_{\Omega ,\nu }(\nu )\) est l’excitance énergétique spectrale (densité spectrale de puissance rayonnée par unité de surface du corps noir). A l’équilibre thermique,
\begin {equation} M_\nu (\nu ,T)=\pi L_{\Omega ,\nu }(\nu ,T)=\frac {2\pi h\nu ^3}{c^2}\frac {1}{e^{\beta h\nu }-1}\,. \end {equation}
On peut alternativement intégrer d’abord sur la fréquence et définir la luminance énergétique (ou radiance) par unité de surface effective du corps noir et d’angle solide :
\begin {equation} L_\Omega =\int _0^\infty d\nu \,L_{\Omega ,\nu }(\nu )=\frac {c}{4\pi }\int _0^\infty d\nu \,\rho (\nu )h\nu f(h\nu )=\frac {c}{4\pi }\eta _\mathrm {r}\,, \end {equation}
laquelle est donc proportionnelle à la densité d’énergie interne du gaz de photons. A la température \(T\),
\begin {equation} L_\Omega (T)=\frac {c}{4\pi }aT^4=\frac {2(\pi kT)^4}{15h^3c^2}\,. \end {equation}
Finalement, toutes intégrations faites,
\begin {equation} M(T)=\pi L_\Omega (T)=\frac {c}{4}\eta _\mathrm {r}(T)=\frac {2\pi ^5}{15h^3c^2}(kT)^4=\sigma T^4\,. \label {eq:stefanboltzmann} \end {equation}
C’est la loi de Stefan-Boltzmann, et \(\sigma =ac/4=2\pi ^5k^4/(15h^3c^2)=5.670\times 10^{-8}\)W/m\(^2\)/K\(^4\) est la constante du même nom. Enfin, on définit la luminosité (ou flux énergétique) comme la puissance totale rayonnée
\begin {equation} L(T)=SM(T)\,, \label {eq:luminosite} \end {equation}
où \(S\) est la surface du corps noir. On retrouvera dans la Table 1.1 les principales grandeurs photométriques introduites dans ce paragraphe.
Nom Description Luminance énergétique, Puissance traversant une unité de
surface dans une direction \((\theta ,\varphi )\) donnée,
par unité d’angle solide Densité de flux radiatif Puissance totale traversant une
unité de surface, Excitance énergétique Densité de flux radiatif sortant, Luminosité Puissance totale rayonnée par une
surface S, \(L=\int _\mathrm {S} d^2\vec {r} M(\vec {r})\) Intensité énergétique Puissance totale rayonnée par unité
d’angle solide [\(I=L/(4\pi )\) pour un
rayonnement isotrope] Eclairement énergétique, Puissance reçue par unité de surfaceUnité
Radiance \(L_\Omega \) W/sr/m\(^2\)
\(F_\mathrm {r}\)
\(F_\mathrm {r}=\int _\text {Sphère} d\Omega \,\cos \theta L_\Omega (\theta ,\varphi )\) W/m\(^2\)
\(M\)
\(M=\int _\text {Hémisphère} d\Omega \,\cos \theta L_\Omega (\theta ,\varphi )\) W/m\(^2\)
\(L\) W
\(I\) W/sr
Irradiance \(E_\mathrm {e}\) W/m\(^2\)
Si au contraire les photons sont réfléchis par des parois de l’enceinte, ils vont exercer sur elles une pression cinétique (comme le font les particules massives)10. En reprenant le raisonnement du paragraphe 1.2.2, il vient :
\begin {align} P_\mathrm {r}&=\int _{\mathbb {R}^3}d^3\vec {k}\,\rho _\vec {k}v_xp_xf(h\nu _k) \nonumber \\ &=\int _{\mathbb {R}^3} d^3\vec {k}\,\rho _k\left (\frac {k_x}{k}c\right )\hbar k_xf(h\nu _k)\,. \end {align}
Cette expression s’intègre facilement en coordonnées sphériques :
\begin {align} P_\mathrm {r}&=\hbar c\int _{0}^{2\pi }d\varphi \int _{0}^{\pi }d\theta \,\sin \theta \cos ^2\theta \int _0^\infty dk\,\rho _k k^3 f(h\nu _k) \nonumber \\ &=\frac {1}{c}\int _{0}^{2\pi }d\varphi \int _{0}^{\pi }d\theta \,\sin \theta \cos ^2\theta \int _0^\infty dk\,\rho _k ck^2 h\nu _k f(h\nu _k) \nonumber \\ &=\frac {1}{c}\int _{0}^{2\pi }d\varphi \int _{0}^{\pi }d\theta \,\sin \theta \cos ^2\theta \int _0^\infty d\nu \,L_{\Omega ,\nu }(\nu )\ \ \ \ \text {[cf. Eq.~\eqref {eq:Mcorpsnoir}]} \nonumber \\ &=\frac {1}{c}\int _{0}^{2\pi }d\varphi \int _{0}^{\pi }d\theta \,\sin \theta \cos ^2\theta \,L_{\Omega } \nonumber \\ &=\frac {4\pi }{3c}L_\Omega =\frac {1}{3}\eta _\mathrm {r}\,. \label {eq:Pradint} \end {align}
La pression de radiation est donc le tiers de la densité d’énergie interne (vs deux tiers pour les fermions massifs non relativistes). A l’équilibre thermodynamique à la température \(T\),
\begin {equation} P_\mathrm {r}(T)=\frac {4\sigma }{3c}T^4=\frac {1}{3}aT^4\,. \label {eq:Prad} \end {equation}
On aura pu remarquer dans la dérivation du rayonnement du corps noir et de la pression de radiation les relations qui unissent les moments de la luminance énergétique
\begin {equation} \hat {\mu }_n(L_\Omega )=\int _{0}^{2\pi }d\varphi \int _{0}^{\pi }d\theta \,\sin \theta \cos ^n\theta L_\Omega (\theta ,\varphi ) \end {equation}
aux différentes grandeurs d’intérêt :
\(\hat {\mu }_0(L_\Omega )=c\eta _\mathrm {r}\),
\(\hat {\mu }_1(L_\Omega )=F_\mathrm {r}\), la densité de flux radiatif qui traverse (toutes directions confondues) une surface dans le gaz de photons.
\(\hat {\mu }_2(L_\Omega )=cP_\mathrm {r}\).
Ces relations sont valables quelle que soit la fonction de distribution \(f(\nu )\) du gaz de photons. Elles peuvent même s’appliquer si cette distribution est anisotrope. Introduisons en effet une fonction de distribution angulaire \(f_\Omega (\theta ,\varphi ,\nu )\) (par unité de fréquence et d’angle solide) avec pour seule contrainte une symétrie axiale \(f_\Omega (\theta ,\varphi ,\nu )=f_\Omega (-\theta ,\varphi ,\nu )=f_\Omega (\theta ,\varphi +\pi ,\nu )\). La luminance énergétique spectrale est alors
\begin {equation} L_{\Omega ,\nu }(\theta ,\varphi ,\nu )=c\rho (\nu )h\nu f_\Omega (\theta ,\varphi ,\nu )\,. \end {equation}
La luminance énergétique reste définie par :
\begin {equation} L_\Omega (\theta ,\varphi )=\int _0^\infty d\nu \,L_{\Omega ,\nu }(\theta ,\varphi ,\nu )\,. \end {equation}
La densité d’énergie par unité de volume, le flux radiatif et la pression de radiation au travers de/sur une surface perpendiculaire à l’axe polaire s’écrivent alors, sur le même modèle qu’aux paragraphes précédents :
\begin {align} \eta _\mathrm {r}&=\int _{0}^{2\pi }d\varphi \int _{0}^{\pi }d\theta \,\sin \theta \int _0^\infty d\nu \,\rho (\nu )h\nu f_\Omega (\theta ,\varphi ,\nu )=\frac {1}{c}\hat {\mu }_0(L_\Omega ) \label {eq:moments1} \\ F_\mathrm {r}&=\int _{0}^{2\pi }d\varphi \int _{0}^{\pi }d\theta \,\sin \theta \cos \theta L_\Omega (\theta ,\varphi )=\hat {\mu }_1(L_\Omega ) \label {eq:moments2} \\ P_\mathrm {r}&=2\int _{0}^{2\pi }d\varphi \int _{0}^{\pi /2}d\theta \,\sin \theta \cos ^2\theta \int _0^\infty d\nu \,\rho (\nu )h\nu f_\Omega (\theta ,\varphi ,\nu )=\frac {1}{c}\hat {\mu }_2(L_\Omega )\,. \label {eq:moments3} \end {align}
Ces relations seront utilisées pour dériver les équations de transfert radiatif au chapitre 2.
Avec sa température de surface11 \(T_\odot =5775\) K, et son rayon \(R_\odot =696\,340\)km, le Soleil [1] modélisé comme un corps noir rayonne12 :
\begin {equation} L_\odot =4\pi R^2\sigma T_\odot ^4=3.84\times 10^{26}\,\text {W}. \end {equation}
L’intensité énergétique (puissance émise par unité d’angle solide) d’une étoile est
\begin {equation} I=\frac {L}{4\pi } \end {equation}
puisque sont rayonnement est isotrope. Un instrument (miroir de téléscope, ...) de surface \(A\) situé à une distance \(d\) de l’étoile est vu depuis celle-ci sous un angle solide13 \(\Omega \approx A/d^2\), et va donc collecter une puissance totale :
\begin {equation} P\approx I\frac {A}{d^2}=\frac {L}{4\pi }\frac {A}{d^2}=AE_\mathrm {e}\,, \end {equation}
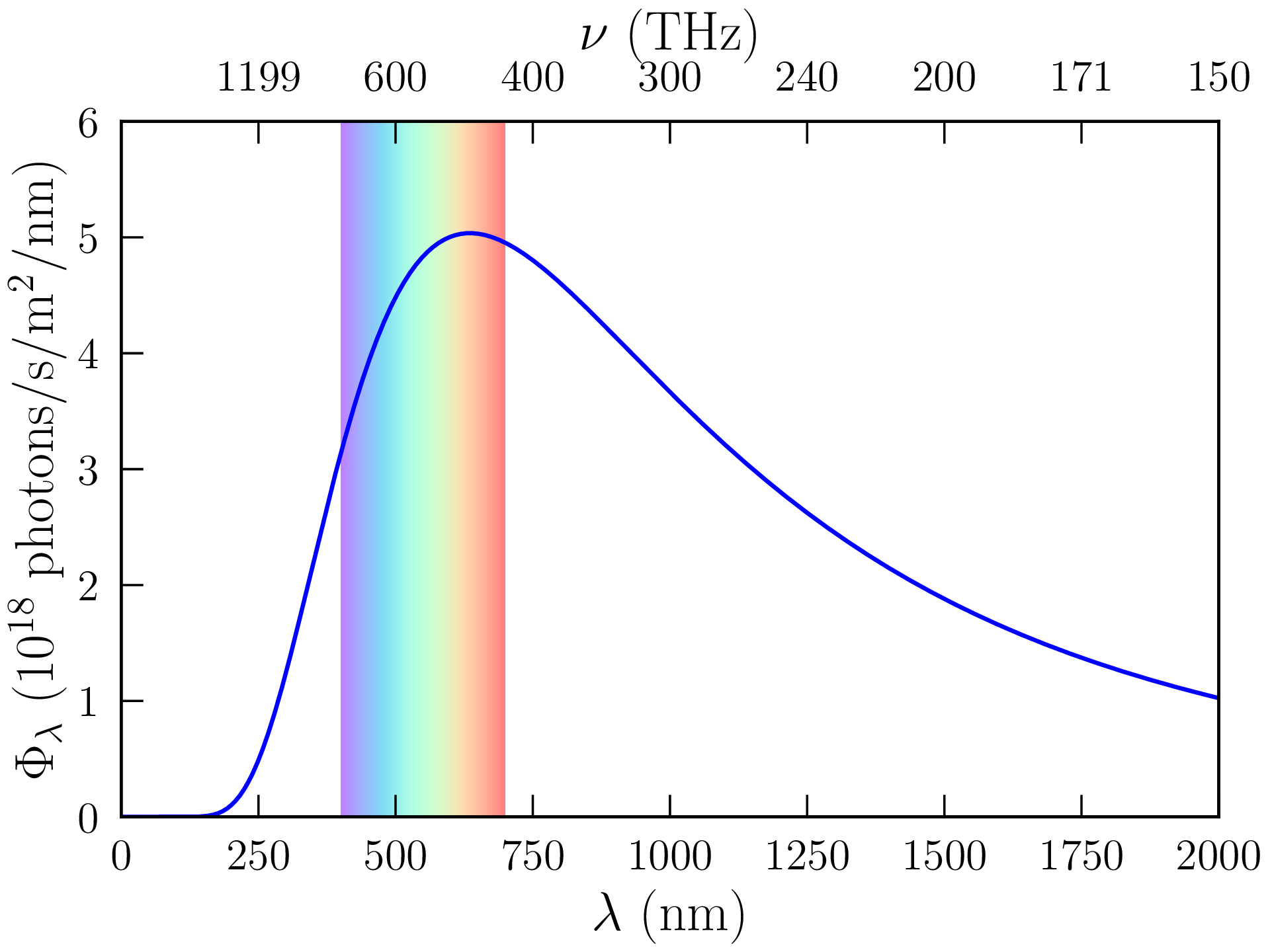
où \(E_\mathrm {e}=L/(4\pi d^2)\) est l’éclairement énergétique ou irradiance (puissance reçue par unité de surface). Cette puissance décroît comme \(1/d^2\) comme attendu de la conservation du flux de photons. En particulier, l’éclairement énergétique du Soleil sur la Terre (\(d_\odot \approx 150\,000\,000\)km) est \(E_\mathrm {e}(\odot )=L_\odot /(4\pi d_\odot ^2)=1360\)W/m\(^2\) (en négligeant l’absorption par l’atmosphère). Le spectre de cette lumière est représenté sur la figure 1.4 (voir le code blackbody.py). On a calculé le nombre de photons arrivant chaque seconde sur une surface terrestre \(A=1\)m\(^2\), par unité de fréquence d’abord,
\begin {equation} \Phi _\nu (\nu )=\frac {1}{h\nu }(4\pi R_\odot ^2)M_{\nu }(\nu ,T_\odot )\frac {1}{4\pi d_\odot ^2}=\frac {1}{h\nu }M_{\nu }(\nu ,T_\odot )\left (\frac {R_\odot }{d_\odot }\right )^2\,, \end {equation}
puis par unité de longueur d’onde :
\begin {equation} \Phi _\lambda (\lambda )=\Phi _\nu \left (\frac {c}{\lambda }\right )\left |\frac {d\nu }{d\lambda }\right |=\frac {1}{h\lambda }M_{\nu }\left (\frac {c}{\lambda },T_\odot \right )\left (\frac {R_\odot }{d_\odot }\right )^2\,. \end {equation}
La forme « en cloche » du spectre de la figure 1.4 est caractéristique d’un corps noir : la quantité de photons émis décroît à haute fréquence/basse longueur d’onde car l’énergie thermique \(kT_\odot \) n’est pas suffisante pour produire de tels photons, et à basse fréquence/grande longueur d’onde parce que la densité de modes \eqref{eq:rhoph} susceptibles de porter ces photons devient trop faible. En pratique, le Soleil présente des raies d’absorption marquées à l’intérieur de son spectre liées aux interactions entre les photons et la matière (en particulier les atomes incomplètement ionisés de la photosphère). La mesure de l’enveloppe « corps noir » du spectre d’une étoile permet de calculer sa température de surface \(T_\mathrm {c}\) (en supposant que les photons émis dans le coeur chaud de l’étoile sont thermalisés lorsqu’ils parviennent à sa surface). Cette température définit donc la couleur de l’étoile (jaune-orangé pour le Soleil). La densité de flux radiatif croissant comme \(T_\mathrm {c}^4\), une étoile deux fois plus chaude que le Soleil va rayonner 16 fois plus (par unité de surface). Plus précisément, la luminosité \(L\), le rayon \(R\), et la température \(T\equiv T_\mathrm {c}\) d’une étoile sont liées à celles (\(L_\odot \), \(R_\odot \), \(T_\odot \)) du Soleil par la relation :
\begin {equation} \frac {L}{L_\odot }=\left (\frac {R}{R_\odot }\right )^2\left (\frac {T}{T_\odot }\right )^4\,. \end {equation}
On définit la magnitude bolométrique d’une étoile à partir de sa luminosité totale :
\begin {equation} M_\mathrm {bol}-M_\mathrm {bol}(\odot )=-2.5\log _{10}\left (\frac {L}{L_\odot }\right )\,. \end {equation}
La magnitude bolométrique du Soleil relève d’un choix, \(M_\mathrm {bol}(\odot )=4.74\). De façon contre-intuitive, la luminosité d’une étoile est d’autant plus faible que sa magnitude est grande. On définit également la magnitude absolue d’une étoile à partir de son éclairement énergétique si elle était situé à une distance de référence \(d_\mathrm {ref}=10\,\text {parsecs}=32.6\,\text {années-lumière}\) :
\begin {equation} M_\mathrm {abs}=-2.5\log _{10}\left (\frac {L}{L_\odot }\frac {1}{4\pi d_\mathrm {ref}^2}\right )+C=-2.5\log _{10}\left (\frac {L}{L_\odot }\right )+C^\prime \,, \end {equation}
où \(C\), \(C^\prime \) sont des constantes. Il est difficile (voir impossible) de mesurer la luminosité réelle d’une étoile car les instruments n’intègrent jamais qu’une partie du spectre. Dans la fenêtre du visible (\(\lambda \equiv 550\pm 44\)nm), on choisit \(C^\prime \) telle que \(M_\mathrm {abs}^\mathrm {v}(\odot )=4.83\), si bien que :
\begin {equation} M_\mathrm {abs}^\mathrm {v}=4.83-2.5\log _{10}\left (\frac {L^\mathrm {v}}{L_\odot ^\mathrm {v}}\right )\,. \end {equation}
Enfin, la magnitude apparente est définie à partir de l’éclairement énergétique mesuré sur Terre :
\begin {equation} M_\mathrm {app}=-2.5\log _{10}\left (\frac {L}{L_\odot }\frac {1}{4\pi d^2}\right )=M_\mathrm {abs}+5(\log _{10}d-1)\,, \end {equation}
où la distance \(d\) est exprimée en parsecs. La magnitude apparente du Soleil dans la bande du visible est donc \(M_\mathrm {app}^\mathrm {v}(\odot )=-26.7\) (\(d_\odot =4.848\times 10^{-6}\) parsecs). L’estimation d’au moins deux quantités (magnitude apparente et distance par exemple) permet en principe de reconstruire la troisième (magnitude absolue). Il faut néanmoins prendre soin de corriger la magnitude apparente mesurée de l’absorption additionnelle par l’atmosphère, les poussières et les gaz interstellaires. On remarquera aussi que la différence de magnitude apparente entre deux corps A et B est simplement :
\begin {equation} M_\mathrm {app}(B)-M_\mathrm {app}(A)=-2.5\log _{10}\left (\frac {E_\mathrm {e}(B)}{E_\mathrm {e}(A)}\right )\,. \end {equation}
En particulier,
\begin {equation} M_\mathrm {app}-M_\mathrm {app}(\odot )=-2.5\log _{10}\left (\frac {E_\mathrm {e}}{E_\mathrm {e}(\odot )}\right )\,. \end {equation}
Il faut toujours adapter \(M_\mathrm {app}(\odot )\) et \(E_\mathrm {e}(\odot )\) à la bande de fréquences effectivement mesurée par les instruments – En particulier, \(M_\mathrm {app}=0\) pour \(E_\mathrm {e}=3.631\times 10^{-2}\)W/m\(^2\) dans la bande du visible.
Deux corps de masse \(m_1\) et \(m_2\) aux positions \(\vec {r}_1\) et \(\vec {r}_2\) s’attirent mutuellement sous l’effet de la gravité ; les forces \(\vec {F}_1\) et \(\vec {F}_2\) qui s’exercent sur ces corps sont (Loi de Newton de la gravitation universelle) :
\begin {equation} \vec {F}_1=-\vec {F}_2=G\frac {m_1 m_2}{r_{12}^3}\vec {r}_{12}\,, \end {equation}
où \(\vec {r}_{12}=\vec {r}_2-\vec {r}_1\), \(r_{12}=|\vec {r}_{12}|\), et \(G=6.674\times 10^{-11}\)N.m\(^2\)/kg\(^2\) est la constante gravitationnelle. La norme de ces forces,
\begin {equation} F=G\frac {m_1 m_2}{r_{12}^2} \end {equation}
décroît comme le carré de la distance qui sépare les deux corps. Ces forces dérivent d’un potentiel scalaire :
\begin {equation} \vec {F}_1=-m_1\boldsymbol {\nabla }_{\vec {r}_1}V_2(r_{12})\ \&\ \vec {F}_2=-m_2\boldsymbol {\nabla }_{\vec {r}_2}V_1(r_{12})\,, \label {eq:fgravite} \end {equation}
où :
\begin {equation} V_i(r)=-G\frac {m_i}{r}\,. \end {equation}
On remarquera l’analogie avec l’électrostatique, à ceci près que les masses, à l’inverse des charges, sont toujours positives (et les forces de gravité toujours attractives). Par extension, la force exercée par une distribution de masse volumique \(\rho (\vec {r})\) sur une masse ponctuelle \(m\) située au point \(\vec {r}\) est :
\begin {equation} \vec {F}=-m\boldsymbol {\nabla }_{\vec {r}}V[\rho ](\vec {r})\,, \end {equation}
où le potentiel gravitationnel de la distribution de masse est :
\begin {equation} V[\rho ](\vec {r})=-G\int _{\mathbb {R}^3}d^3\vec {r}^\prime \,\frac {\rho (\vec {r}^\prime )}{|\vec {r}-\vec {r}^\prime |}\,. \label {eq:Vgravite} \end {equation}
On peut aussi définir une énergie potentielle interne de pesanteur \(U_\mathrm {g}[\rho ]\) comme le travail qu’il a fallu fournir pour construire adiabatiquement la distribution de masse \(\rho (\vec {r})\). Comme cette énergie interne ne doit pas dépendre du chemin suivi, on suppose ramener depuis l’infini des masses élémentaires \(dm=Md\alpha \) (avec \(M\) la masse totale), que l’on répartit suivant le modèle de la distribution \(\rho (\vec {r})\) ; le travail fourni au cours de cette opération est :
\begin {equation} dW(\alpha )=d\alpha \int _{\mathbb {R}^3}d^3\vec {r}\,\rho (\vec {r})V[\alpha \rho ](\vec {r})\,, \end {equation}
où \(V[\alpha \rho ](\vec {r})=\alpha V[\rho ](\vec {r})\) est le potentiel créé par la distribution de masse \(\alpha \rho (\vec {r})\). Le travail total fourni est donc :
\begin {equation} W=\int _0^1 d\alpha \,\frac {dW}{d\alpha }\,, \end {equation}
si bien que :
\begin {equation} U_\mathrm {g}[\rho ]=W=\frac {1}{2}\int _{\mathbb {R}^3}d^3\vec {r}\,\rho (\vec {r})V[\rho ](\vec {r})=-\frac {G}{2}\int _{\mathbb {R}^3}d^3\vec {r}\,\int _{\mathbb {R}^3}d^3\vec {r}^\prime \,\frac {\rho (\vec {r})\rho (\vec {r}^\prime )}{|\vec {r}-\vec {r}^\prime |}\,, \label {eq:Upot} \end {equation}
qui s’interprète comme la somme des interactions de paires entre masses élémentaires \(\rho (\vec {r})d^3\vec {r}\) et \(\rho (\vec {r}^\prime )d^3\vec {r}^\prime \), le facteur \(\tfrac {1}{2}\) corrigeant le double comptage \(\vec {r}\leftrightarrow \vec {r}^\prime \).
Si la densité de masse \(\rho (\vec {r})\equiv \rho (r)\) a la symétrie sphérique (comme c’est le cas pour une étoile), le potentiel \(V[\rho ](\vec {r})\equiv V[\rho ](r)\) l’a aussi. Il est bien plus aisé de traiter ce problème dans sa forme différentielle. En injectant la relation
\begin {equation} \Delta _\vec {\vec {r}}\frac {1}{|\vec {r}-\vec {r}^\prime |}=-4\pi \delta (\vec {r}-\vec {r}^\prime )\ \end {equation}
dans le potentiel \eqref{eq:Vgravite}, il vient :
\begin {equation} \Delta _{\vec {r}}V[\rho ](\vec {r})=4\pi G\rho (\vec {r})\,, \end {equation}
en parfaite analogie encore avec l’équation de Poisson en électrostatique. En coordonnées et en symétrie sphériques, le potentiel \(V[\rho ](r)\) vérifie donc l’équation différentielle :
\begin {equation} \frac {1}{r^2}\frac {d}{dr}\left (r^2\frac {d}{dr}V[\rho ](r)\right )=4\pi G\rho (r)\,. \end {equation}
On peut multiplier les deux membres par \(r^2\) et intégrer sur \(r\). En admettant que \(r^2dV(r)/dr\) tends vers 0 lorsque \(r\to 0\) (à vérifier a posteriori),
\begin {equation} r^2\frac {d}{dr}V[\rho ](r)=4\pi G\int _0^r dr^\prime \,r^{\prime 2}\rho (r^\prime )\,. \end {equation}
On reconnaît à droite la masse totale \({\cal M}[\rho ](r)\) contenue dans la sphère de rayon \(r\) :
\begin {equation} {\cal M}[\rho ](r)=\int _0^{2\pi }d\varphi \,\int _0^{\pi }d\theta \,\sin \theta \int _0^r dr^\prime \,r^{\prime 2}\rho (r^\prime )=4\pi \int _0^r dr^\prime \,r^{\prime 2}\rho (r^\prime )\,. \end {equation}
On obtient ainsi une relation entre le gradient de potentiel et la masse enclose dans cette sphère :
\begin {equation} \frac {d}{dr}V[\rho ](r)=\frac {G{\cal M}[\rho ](r)}{r^2}\,. \end {equation}
La force radiale qui s’excerce sur une masse test \(m_\mathrm {t}\) est donc :
\begin {equation} F(r)=m_\mathrm {t}\frac {\partial ^2r}{\partial t^2}=-m_\mathrm {t}\frac {d}{dr}V[\rho ](r)=-m_\mathrm {t}g[\rho ](r)\,, \end {equation}
où :
est l’accélération centripète subie dans le champ de pesanteur de la distribution de masse \(\rho (r)\). L’énergie potentielle interne de pesanteur de cette distribution est enfin (en supposant \(V[\rho ](r\to \infty )\to 0\)) :
\begin {equation} U_\mathrm {g}[\rho ]=\frac {1}{2}\int _{\mathbb {R}^3}d^3\vec {r}\,\rho (r)V[\rho ](r)=2\pi \int _0^\infty dr\,r^2\rho (r)\int _\infty ^r dr^\prime \,g[\rho ](r^\prime )\,. \end {equation}
Pour une sphére homogène de rayon \(R\) et de masse \(M\), on trouve aisément :
\begin {equation} U_\mathrm {g}=-\frac {3}{5}\frac {GM^2}{R}\,. \label {eq:Ugsphere} \end {equation}
A quelle condition un objet, caractérisé par sa distribution de masse \(\rho (\vec {r})\), et soumis à sa propre pesanteur, est-il en équilibre? Pour répondre à cette question, nous allons supposer que cet objet est au repos14 et n’oppose aucune résistance à la déformation (fluide idéal dans la limite « hydrostatique »). Les forces de pesanteur dérivant d’un potentiel central, rien ne brise la symétrie isotrope de l’espace, aussi la distribution de masse \(\rho (\vec {r})\equiv \rho (r)\) doit-elle adopter une forme sphérique. Imaginons isoler un élément de volume \(dV=dSdr\) de l’objet à la distance \(r\) du centre. Cet élément est soumis à la pression \(P\) de la matière et du rayonnement qui l’entoure, et à son propre poids dans le champ de pesanteur. Par symétrie, la résultante des forces qui s’exercent sur les parois latérales de l’élément de volume est nulle ; les forces radiales qu’il subit sont :
La force de pression sur sa face supérieure \(F_\mathrm {sup}=-P(r+dr)dS\),
La force de pression sur sa face inférieure \(F_\mathrm {inf}=P(r)dS\),
Son poids \(F=-(\rho (r)drdS)g[\rho ](r)\).
A l’équilibre hydrostatique, la somme de ces forces doit être nulle :
\begin {equation} [P(r+dr)-P(r)]dS=-\rho (r)g[\rho ](r)drdS\,. \end {equation}
La pression doit donc vérifier l’équation différentielle :
\begin {equation} \frac {d}{dr}P(r)=-\rho (r)g[\rho ](r)=-\rho (r)\frac {G{\cal M}[\rho ](r)}{r^2}\,. \label {eq:hydro} \end {equation}
Introduisons maintenant une masse test \(m_\mathrm {t}\) dans le fluide (sous la forme d’un un solide indéformable de volume \(\delta V=\delta S\delta r\) et de densité homogène \(\rho _\mathrm {t}\)). Où cette masse est-elle dans une position stable? La force radiale qu’elle subit, appelée « poussée d’Archimède » est, à l’instar du raisonnement précédent,
\begin {equation} F=[P(r)-P(r+\delta r)]\delta S-\rho _\mathrm {t}g[\rho ](r)\delta r\delta S\,. \end {equation}
Si le fluide reste à l’équilibre hydrostatique, \(dP/dr=-\rho (r)g[\rho ](r)\), si bien que :
\begin {equation} F\approx [\rho (r)-\rho _\mathrm {t}]g[\rho ](r)\delta V\,. \end {equation}
Par conséquent, la masse test coule si elle est plus dense que le fluide, monte si elle est moins dense, et est à l’équilibre lorsque \(\rho _\mathrm {t}=\rho (r)\) (ou, si elle n’est pas complètement immergée, lorsqu’elle a déplacé un volume de fluide de même poids). Cet équilibre est stable si et seulement si \(\rho (r)\) est une fontion décroissante de \(r\) (déplacée vers le bas, dans un milieu plus dense, ou vers le haut, dans un milieu moins dense, la masse est rappelée vers son point d’équilibre par la poussée d’Archimède). En appliquant cet argument au fluide lui-même, on conclut que l’équilibre hydrostatique n’est stable que si \(d\rho /dr<0\). Bien que ce soit généralement vrai, il faut garder à l’esprit que le fluide n’est pas indéformable, et donc qu’un volume test déplacé hors équilibre va voir sa densité changer (cf. instabilité convective au chapitre 2). Les critères de stabilité de l’équilibre hydrostatique sont donc intimement liés à l’équation d’état du fluide et peuvent être très complexes.
Dans un objet dégénéré, la pression ne dépend essentiellement que de la densité d’électrons [\(P\propto n^{5/3}\) dans un gaz non-relativiste, Eq. \eqref{eq:Pdeg}, et \(P\propto n^{4/3}\) dans un gaz ultra-relativiste, Eq. \eqref{eq:Pdegurel}]. En supposant que cet objet soit localement à l’équilibre thermodynamique et puisse être caractérisé par une pression \(P(r)\) et une densité \(n(r)\) liées par Eqs. \eqref{eq:Pdeg} ou \eqref{eq:Pdegurel}, la condition d’équilibre hydrostatique \eqref{eq:hydro} devient une équation structurale pour la densité dans l’objet.
De façon générale, on peut considérer un « polytrope » caractérisé par l’équation d’état \(P(\rho )=C\rho ^\gamma \), où \(\rho =nm\) est la densité de masse et \(m\) la masse des particules. L’exposant \(\gamma \) est appelé indice adiabatique, qu’il est commode de mettre sous la forme \(\gamma =1+1/p\), où \(p\) est l’indice polytropique. L’équation \eqref{eq:hydro} s’écrit alors :
\begin {align} &C\gamma \rho (r)^{\gamma -1}\frac {d}{dr}\rho (r)=-\rho (r)\frac {G}{r^2}\int _0^r dr^\prime \,4\pi r^{\prime 2}\rho (r^\prime ) \nonumber \\ \Rightarrow \ &C(1+p)r^2\frac {d}{dr}\rho (r)^{1/p}=-G\int _0^r dr^\prime \,4\pi r^{\prime 2}\rho (r^\prime )\,. \end {align}
En dérivant de nouveau par rapport à \(r\), il vient :
\begin {equation} C(1+p){r^2}\frac {d}{dr}\left (r^2\frac {d}{dr}\rho (r)^{1/p}\right )=-4\pi G\rho (r)\,. \end {equation}
On peut ensuite faire les changements de variable suivants pour adimensionnaliser cette équation différentielle :
\begin {align} w_p(r)&=\left (\frac {\rho (r)}{\rho (0)}\right )^{1/p} \\ z&=\alpha _p r\text { avec }\alpha _p^2=\frac {4\pi G}{C(1+p)}\rho (0)^{(p-1)/p}\,. \end {align}
On obtient ainsi l’équation de Lane-Emden :
\begin {equation} \frac {1}{z^2}\frac {d}{dz}\left (z^2\frac {d}{dz}w_p(z)\right )+w_p(z)^p=0\,, \label {eq:LaneEmden} \end {equation}
avec les conditions aux limites \(w_p=1\) et \(dw_p/dz=0\) en \(z=0\). Il existe quelques valeurs de \(p\) (\(p=0\), \(p=1\), \(p=5\)) pour lesquelles la solution est analytique [2]. Pour \(p=1\) (\(\gamma =2\)) par exemple,
\begin {equation} w_1(z)=\frac {\sin z}{z}\,. \end {equation}
Le rayon \(R\) de l’objet est défini par le premier zéro \(z_p=\alpha _p R\) de la fonction \(w_p(z)\) (\(z_1=\pi \)). On peut montrer que la solution de l’équation \eqref{eq:LaneEmden} n’a pas de zéros si \(p>5\), auquel cas l’objet reste diffus. Pour \(p<5\), on peut établir une relation entre la masse \(M\) et le rayon \(R\) de l’objet :
\begin {align} M&=\int _0^R dr^\prime \,4\pi r^{\prime 2}\rho (r^\prime ) \nonumber \\ &=\frac {4\pi }{\alpha _p^3}\rho (0)\int _0^{z_p} dz\,z^2w_p(z)^p \nonumber \\ &=-\frac {4\pi }{\alpha _p^3}\rho (0)z_p^2\frac {dw_p}{dz}(z_p)\,. \label {eq:MRpolytrope} \end {align}
Par conséquent, \(\rho (0)\propto M^{2p/(3-p)}\) puisque \(\alpha _p\propto \rho (0)^{(p-1)/(2p)}\), et :
\begin {equation} R=\frac {z_p}{\alpha _p}\propto M^{(1-p)/(3-p)}\,. \end {equation}
Le rayon du polytrope croît donc avec sa masse quand \(0\le p<1\) (\(\gamma >2)\). La pression exercée par les gaz augmente en effet plus vite que leur poids lors d’un accroissement de masse à rayon constant, entraînant la dilatation du polytrope. A l’inverse, le rayon décroît avec la masse quand \(1<p<3\) (\(\tfrac {4}{3}<\gamma <2\)), car le poids augmente plus vite que la pression des gaz (mais \(R\) reste fini pour toute masse \(M\) finie). C’est le cas en particulier pour les gaz dégénérés non relativistes. Le rayon est indépendant de \(M\) pour \(p=1\) (\(\gamma =2\)). Le rayon du polytrope croît également avec sa masse quand \(3<p<5\) (\(\tfrac {6}{5}<\gamma <\tfrac {4}{3}\)), mais de tels objets sont dynamiquement instables. En fait, l’équilibre hydrostatique n’est stable que pour \(p<3\). Le cas limite \(p=3\) (\(\gamma \to \tfrac {4}{3}\)) est particulièrement intéressant puisqu’il correspond aux gaz dégénérés ultra-relativistes.
Si \(\gamma =\tfrac {4}{3}\), \(M\propto R^0\) est indépendante du rayon et vaut d’après \eqref{eq:MRpolytrope} :
\begin {equation} M_\mathrm {C}=-4\pi \left (\frac {C}{\pi G}\right )^{3/2}z_3^2\frac {dw_3}{dz}(z_3) \end {equation}
appelée masse de Chandrasekhar. Dans le cas d’un gaz ultra-relativiste [Eq. \eqref{eq:Pdegurel}],
\begin {equation} C=\frac {\hbar c}{4}\left (\frac {6\pi ^2}{n_s}\right )^{1/3}\left (\frac {1}{\mu _e m_\mathrm {H}}\right )^{4/3} \end {equation}
où on a écrit \(m=\mu _e m_\mathrm {H}\), avec \(\mu _e\) la masse moléculaire moyenne par électron et \(m_\mathrm {H}\) la masse de l’atome d’hydrogène (\(\mu _e\approx A/Z\) pour un gaz de l’élément à \(A\) nucléons dont \(Z\) protons). A partir de la solution numérique pour \(w_3\) et \(z_3\), on obtient, tous calculs faits :
\begin {equation} M_\mathrm {C}=1.44\left (\frac {2}{\mu _e}\right )^2M_\odot \,. \label {eq:Chandrasekhar} \end {equation}
Seul un objet de cette masse (mais de rayon \(R\) arbitraire15) peut donc satisfaire l’équation de Lane-Emden pour \(\gamma =\tfrac {4}{3}\). Cette « singularité » doit être interprétée avec soin. Tout d’abord, les indices adiabatiques \(\gamma =\tfrac {5}{3}\) (gaz dénégéré non relativiste) et \(\gamma =\tfrac {4}{3}\) (gaz dégénéré ultra-relativiste) sont des cas limites qui se cotoient à l’intérieur de l’objet (sa surface étant de facto non relativiste). Le caractère relativiste du gaz augmente au fur et à mesure que la masse de l’objet croît, et ce d’autant plus vite que son rayon diminue et que la densité augmente. On peut résoudre la condition d’équilibre hydrostatique \eqref{eq:hydro} pour un gaz arbitraitement relativiste satisfaisant l’équation d’état \eqref{eq:Pdegrel} (voir le code Chandrasekhar.py). On montre (figure 1.5) que le rayon \(R\) de l’objet tend vers zéro lorsque \(M\to M_\mathrm {C}\) : la masse de Chandrasekhar apparaît donc comme la masse limite que peut avoir un objet soutenu par la seule pression de dégénérescence des électrons avant qu’il ne s’effondre complètement. En pratique, l’objet va se transformer avant même d’avoir atteint cette masse, son rayon ne pouvant physiquement tendre vers zéro.
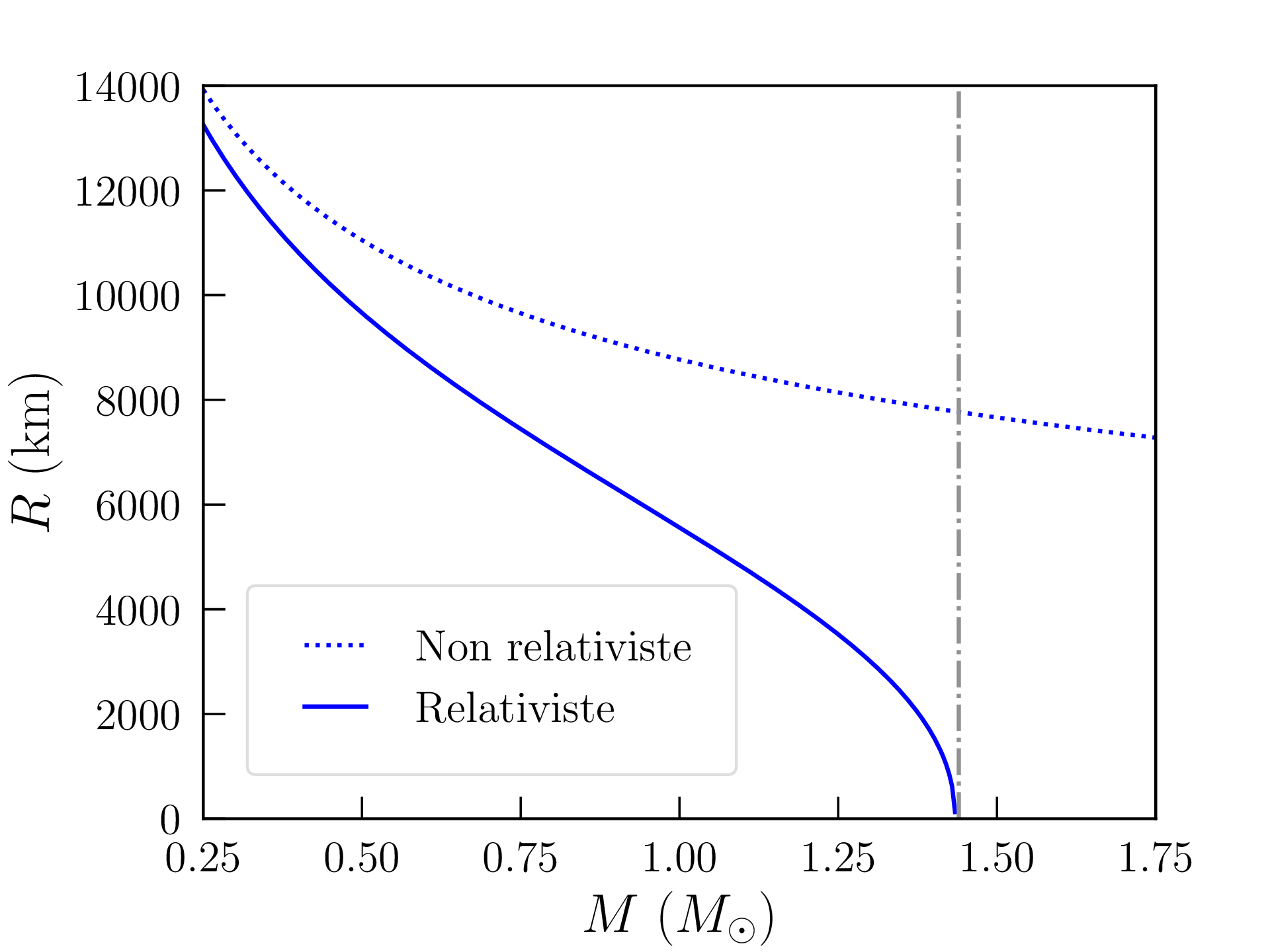
Les naînes blanches sont des « cadavres » d’étoiles légères, correspondant peu ou prou aux cendres dégénérées de leur coeur, généralement composées de carbone et d’oxygène (voir paragraphe 1.5 et chapitre 3). La masse de ces naînes blanches ne peut donc dépasser \(M_\mathrm {C}=1.44M_\odot \) (\(A/Z=2\)). Une naîne blanche qui accrète de la matière et s’approche de cette masse limite finit par s’effondrer ; l’énergie potentielle de pesanteur ainsi libérée la réchauffe jusqu’à ce que démarre la fusion du carbone et de l’oxygène, qui s’emballe car la pression est indépendante de la température dans un gaz dégénéré (donc les réactions nucléaires ne peuvent stopper l’effondrement avant qu’une grande partie de l’étoile ne s’embrase). L’explosion qui s’ensuit libère une formidable quantité d’énergie et disperse la naîne blanche (supernova thermonucléaire de type I).
Une étoile est donc une structure auto-gravitante qui tend à s’effondrer sur elle-même sous l’effet de son propre poids. A l’équilibre hydrostatique \eqref{eq:hydro}, les forces de pesanteur sont contrebalancées par la pression du gaz \eqref{eq:gazparfaits} et du rayonnement \eqref{eq:Prad} qui sont proportionnelles à (une puissance de) leur température. Comme une étoile rayonne, elle dissipe de l’énergie, prélevée (en l’absence d’autres sources16) sur son énergie potentielle interne de pesanteur \eqref{eq:Upot} ; l’étoile se contracte donc progressivement et devrait laisser place in fine à un résidu dégénéré17 très dense et chaud qui va ensuite se refroidir lentement (la pression des gaz dégénérés étant largement indépendante de leur température). Toutefois, des réactions de fusion nucléaire (assemblage de noyaux légers en élements plus lourds) s’amorcent dès que la température au coeur de l’étoile atteint une dizaine de millions de degrés Kelvin. Elles libèrent de l’énergie qui chauffe l’étoile et maintient l’équilibre entre les forces de pesanteur et la pression de la matière et du rayonnement tant que le « combustible » de ces réactions n’est pas épuisé.
La fusion de deux noyaux réclame des températures d’autant plus élevées qu’ils sont chargés (leur impulsion devant, en particulier, être suffisante pour qu’ils s’approchent à portée de l’interaction forte qui va les lier malgré la répulsion Coulombienne). Elle démarre donc naturellement avec l’hydrogène (plus exactement, les protons), élément à la fois le plus abondant et le plus léger dans les étoiles. La fusion de quatre protons produit un noyau d’hélium (particule \(\alpha \)) selon des chemins réactionnels détaillés ci-dessous. La plupart des étoiles passent ainsi l’essentiel de leur vie sur la « séquence principale » où elles brûlent de l’hydrogène en hélium. Lorsque l’hydrogène s’épuise, le coeur de l’étoile se contracte de nouveau sous l’effet de la pesanteur qui reprend l’avantage. Sa température augmente alors jusqu’à permettre éventuellement la fusion de l’hélium en carbone et en oxygène. Le processus peut se poursuivre (en fonction de la masse initiale de l’étoile) jusqu’à la nucléosynthèse du fer, élément le plus stable. Au delà du fer, les processus de fusion sont endothermiques et ne permettent donc plus d’alimenter l’étoile en énergie. La nucléosynthèse des noyaux plus lourds que le fer se déroule dans des conditions particulières (capture rapide de neutrons dans les supernovas, ...) qui seront brièvement introduits ci-dessous.
La fusion de l’hydrogène en hélium sur la séquence principale se déroule selon deux voies distinctes : la chaîne proton-proton et le cycle « catalytique » carbone-azote-oxygène (cycle CNO).
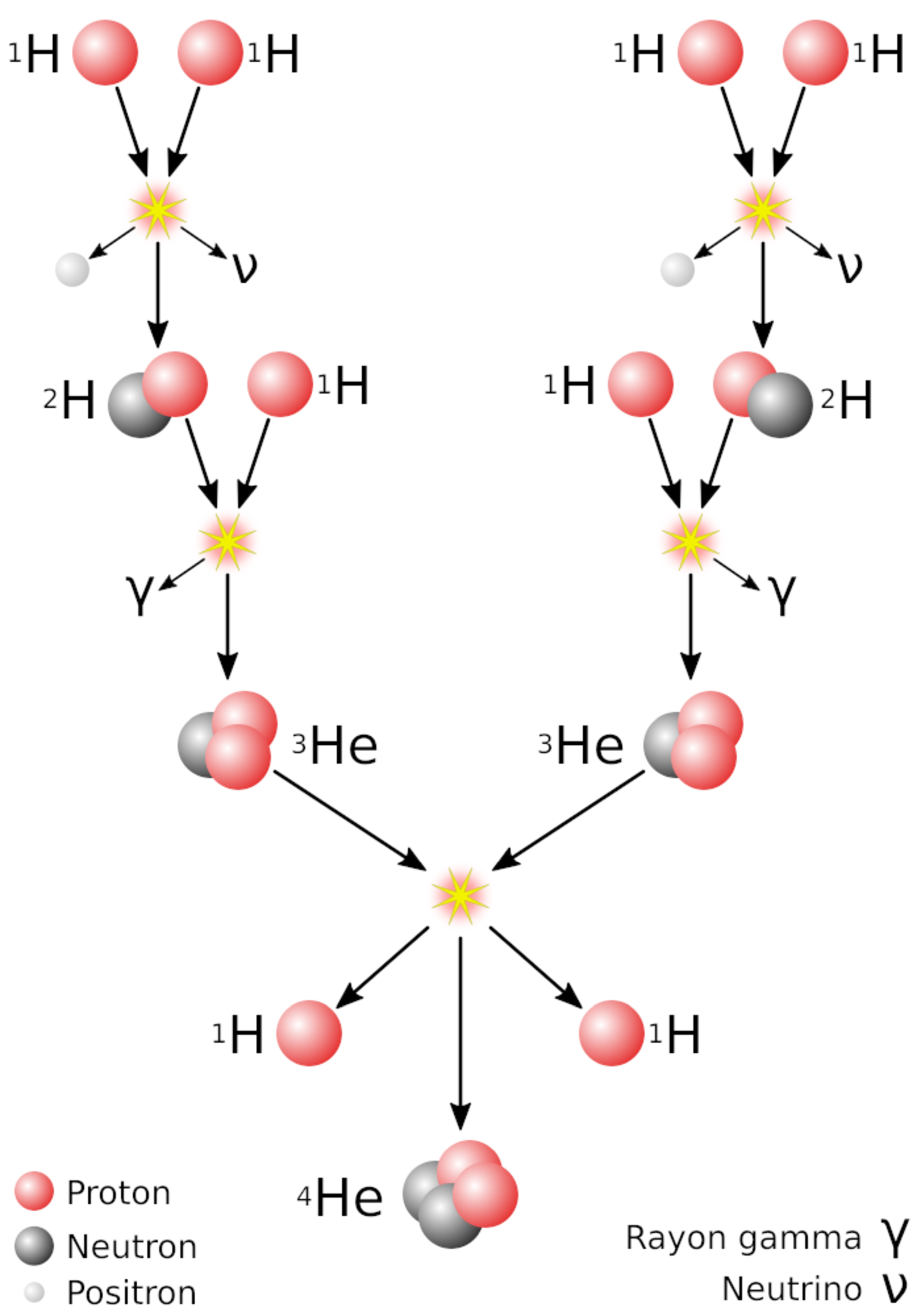
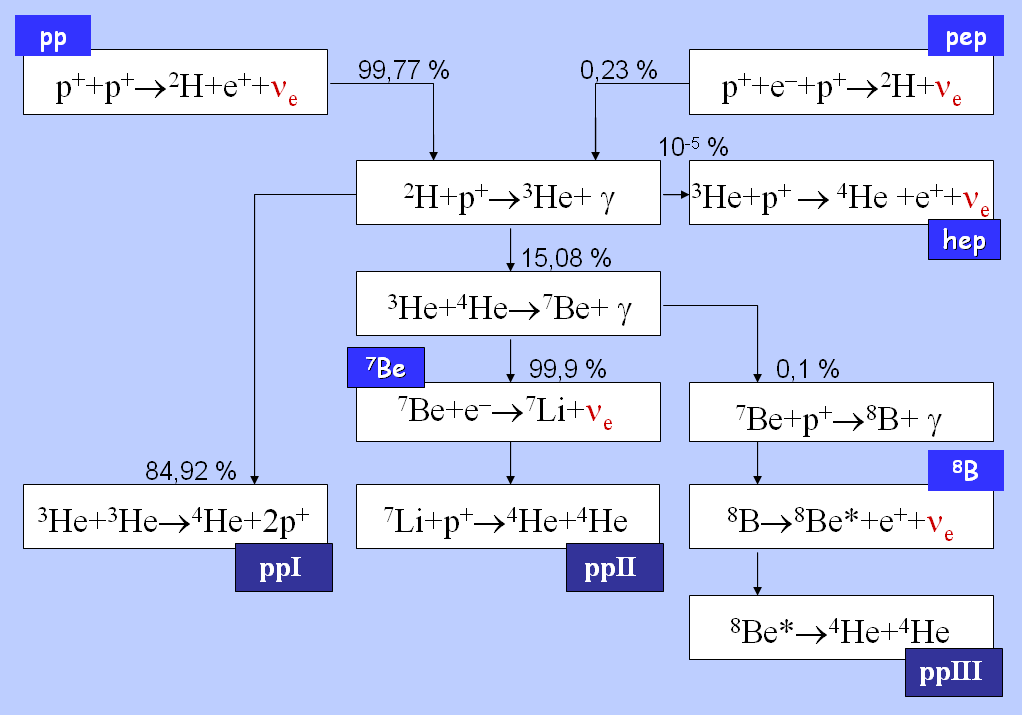
La chaîne proton-proton (PP) est le mécanisme privilégié de fusion de l’hydrogène dans les étoiles de faible masse telles que le Soleil. Elle commence par la fusion de trois protons (\(\ce {^{1}_{1}H}\)) en hélium 3 (\(\ce {^{3}_{2}He}\)). Ces noyaux d’hélium 3 vont ensuite suivre différents chemins réactionnels (branches PP1, PP2, PP3) aboutissant tous à la synthèse d’hélium 4 (\(\ce {^{4}_{2}He}\)). Les premières étapes de la chaîne PP, communes à toutes les branches, sont :
\begin {align} &\ce {^{1}_{1}H}+\ce {^{1}_{1}H}+\rightarrow \ce {^{2}_{1}D}+e^++\nu _\mathrm {e}&(+0.42\mathrm {\ MeV}) \nonumber \\ &e^++e^-\rightarrow 2\gamma &(+1.022\mathrm {\ MeV}) \nonumber \\ &\ce {^{2}_{1}D}+\ce {^{1}_{1}H}\rightarrow \ce {^{3}_{2}He}+\gamma &(+5.493\mathrm {\ MeV}) \end {align}
L’énergie libérée est dissipée par les photons, les neutrinos et l’impulsion des particules. La
fusion proton-proton est l’étape la plus limitante du processus. D’une part, les deux protons
doivent tunneler au travers de la barrière Coulombienne qui les repousse pour entrer dans le puits
d’interaction forte résiduelle qui va les lier. C’est pourquoi de telles réaction de fusion ne peuvent
se produire qu’à des températures supérieures à une dizaine de millions de Kelvin où les
protons ont assez d’énergie cinétique (\(\simeq \tfrac {3}{2}kT\)) pour s’approcher suffisamment. D’autre part,
l’interaction faible doit agir rapidement au contact des protons pour transformer l’un
d’entre eux en neutron, sinon ils se séparent. La durée de vie moyenne d’un proton
dans le Soleil (avant qu’il ne fusionne avec un autre proton) serait ainsi de \(\approx 9\) milliards
d’années. La durée de vie du deutérium \(\ce {^{2}_{1}D}\) (avant qu’il ne soit transformé en hélium \(\ce {^{3}_{2}He}\)) est, à
l’inverse, de l’ordre de la seconde. La chaîne PP s’arrête essentiellement à ce stade
tant que la concentration en \(\ce {^{3}_{2}He}\) n’est pas suffisante pour alimenter PP1, PP2 ou PP3.
Branche PP1
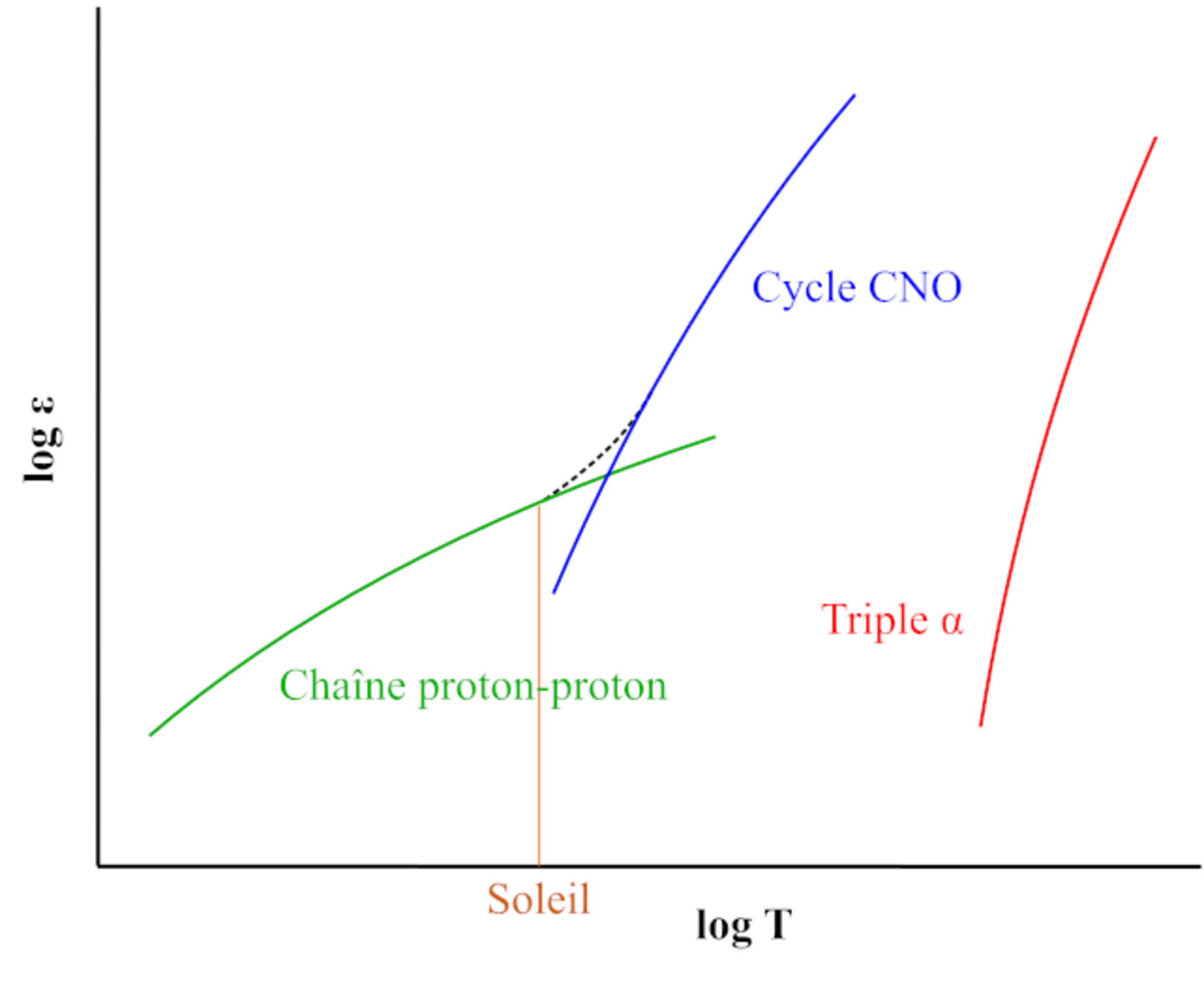
PP1 est le mécanisme de nucléosynthèse de \(\ce {^{4}_{2}He}\) dominant pour des températures de \(10\) à \(18\times 10^6\)K (Fig. 1.6).
Il s’agit de la fusion de deux noyaux \(\ce {^{3}_{2}He}\) accompagnée de la libération de deux protons « rendus » au
combustible :
\begin {align} &\ce {^{3}_{2}He}+\ce {^{3}_{2}He}\rightarrow \ce {^{4}_{2}He}+2\ce {^{1}_{1}H}&(+12.859\mathrm {\ MeV}) \end {align}
Le bilan total de la branche PP1 est donc :
\begin {align} &4\ce {^{1}_{1}H}+2e^-\rightarrow \ce {^{4}_{2}He}+6\gamma +2\nu _\mathrm {e} \end {align}
La branche PP1 libère ainsi \(2\times (0.42+1.022+5.493)+12.859=26.73\)MeV par noyau \(\ce {^{4}_{2}He}\) produit, dont 2.2% (0.59 MeV) dans les
neutrinos18.
Branche PP2
PP2 domine pour des températures de \(18\) à \(25\times 10^6\)K et requiert la présence d’un premier noyau
\(\ce {^{4}_{2}He}\) :
\begin {align} &\ce {^{3}_{2}He}+\ce {^{4}_{2}He}\rightarrow \ce {^{7}_{4}Be}+\gamma &(+1.59\mathrm {\ MeV}) \nonumber \\ &\ce {^{7}_{4}Be}+e^-\rightarrow \ce {^{7}_{3}Li}+\nu _\mathrm {e}&(+0.861\mathrm {\ MeV}) \nonumber \\ &\ce {^{7}_{3}Li}+\ce {^{1}_{1}H}\rightarrow 2\ce {^{4}_{2}He}&(+17.35\mathrm {\ MeV}) \end {align}
La branche PP2 libère donc également \(0.42+1.022+5.493+1.59+0.862+17.35=26.73\)MeV par noyau \(\ce {^{4}_{2}He}\) produit (dont \(0.861\)MeV dans le neutrino
émis après la capture d’un électron par le beryllium).
Branche PP3
PP3 domine au delà de \(25\times 10^6\)K et commence comme PP2, mais le destin du beryllium est
différent :
\begin {align} &\ce {^{3}_{2}He}+\ce {^{4}_{2}He}\rightarrow \ce {^{7}_{4}Be}+\gamma \nonumber \\ &\ce {^{7}_{4}Be}+\ce {^{1}_{1}H}\rightarrow \ce {^{8}_{5}B}+\gamma \nonumber \\ &\ce {^{8}_{5}B}\rightarrow \ce {^{8}_{4}Be}+e^++\nu _\mathrm {e} \nonumber \\ &\ce {^{8}_{4}Be}\rightarrow 2\ce {^{4}_{2}He} \end {align}
La chaîne PP3 libère, comme PP1 et PP2, \(26.73\)MeV par noyau \(\ce {^{4}_{2}He}\) produit (en incluant l’annihilation
du positron), mais en grande partie (jusqu’à \(14.06\)MeV) dans le neutrino issu de la désintégration \(\beta ^+\) du
Bore.
On notera que les éléments légers Be, Li et B sont instables à haute température ou
consommés par les réactions de fusion (PP2, PP3), ce qui explique leur faible abondance
dans l’univers. La branche PP1 représente 85% des réactions de fusion au coeur du
Soleil (Fig. 1.6), tandis la branche PP3, bien que peu empruntée, est la source des
neutrinos de plus haute énergie. La durée de vie moyenne d’un noyau \(\ce {^{3}_{2}He}\) dans le Soleil est de
\(400\)ans.
Le cycle carbone-azote-oxygène (CNO) est un mécanisme de fusion où le carbone sert de catalyseur (Fig. 1.7) :
\begin {align} &\ce {^{12}_{6}C}+\ce {^{1}_{1}H}\rightarrow \ce {^{13}_{7}N}+\gamma &(+1.95\mathrm {\ MeV}) \nonumber \\ &\ce {^{13}_{7}N}\rightarrow \ce {^{13}_{6}C}+e^++\nu _\mathrm {e}&(+2.22\text {\ MeV, demie-vie 10 min.}) \nonumber \\ &\ce {^{13}_{6}C}+\ce {^{1}_{1}H}\rightarrow \ce {^{14}_{7}N}+\gamma &(+7.54\mathrm {\ MeV}) \nonumber \\ &\ce {^{14}_{7}N}+\ce {^{1}_{1}H}\rightarrow \ce {^{15}_{8}O}+\gamma &(+7.35\mathrm {\ MeV}) \nonumber \\ &\ce {^{15}_{8}O}\rightarrow \ce {^{15}_{7}N}+e^++\nu _\mathrm {e}&(+2.75\text {\ MeV, demie-vie 2 min.}) \nonumber \\ &\ce {^{15}_{7}N}+\ce {^{1}_{1}H}\rightarrow \ce {^{12}_{6}C}+\ce {^{4}_{2}He}&(+4.96\mathrm {\ MeV}) \end {align}
Le carbone est recyclé et la réaction libère toujours \(26.73\)MeV par noyau \(\ce {^{4}_{2}He}\) produit (les énergies reportées ci-dessus incluent l’annihilation des positrons). Une partie de cette énergie est dissipée par les neutrinos (en moyenne \(1.7\)MeV). La barrière Coulombienne à la fusion étant nettement plus élevée que dans la chaîne proton-proton, le cycle CNO démarre à bien plus haute température (\(T>15\times 10^6\)K), mais son rendement croît très vite (Fig. 1.8) car il ne nécessite pas la transformation rapide d’un proton en neutron par l’interaction faible comme pour la nucléosynthèse du deutérium \(\ce {^{2}_{1}D}\). Ce rendement est également proportionnel à la métallicité de l’étoile (la concentration d’éléments plus lourds que H/He, dont le carbone, voir chapitre 2). La capture du proton par \(\ce {^{14}_{7}N}\) est l’étape la plus limitante du processus. Le cycle CNO représenterait 1.7% de la production de \(\ce {^{4}_{2}He}\) dans le Soleil [4].
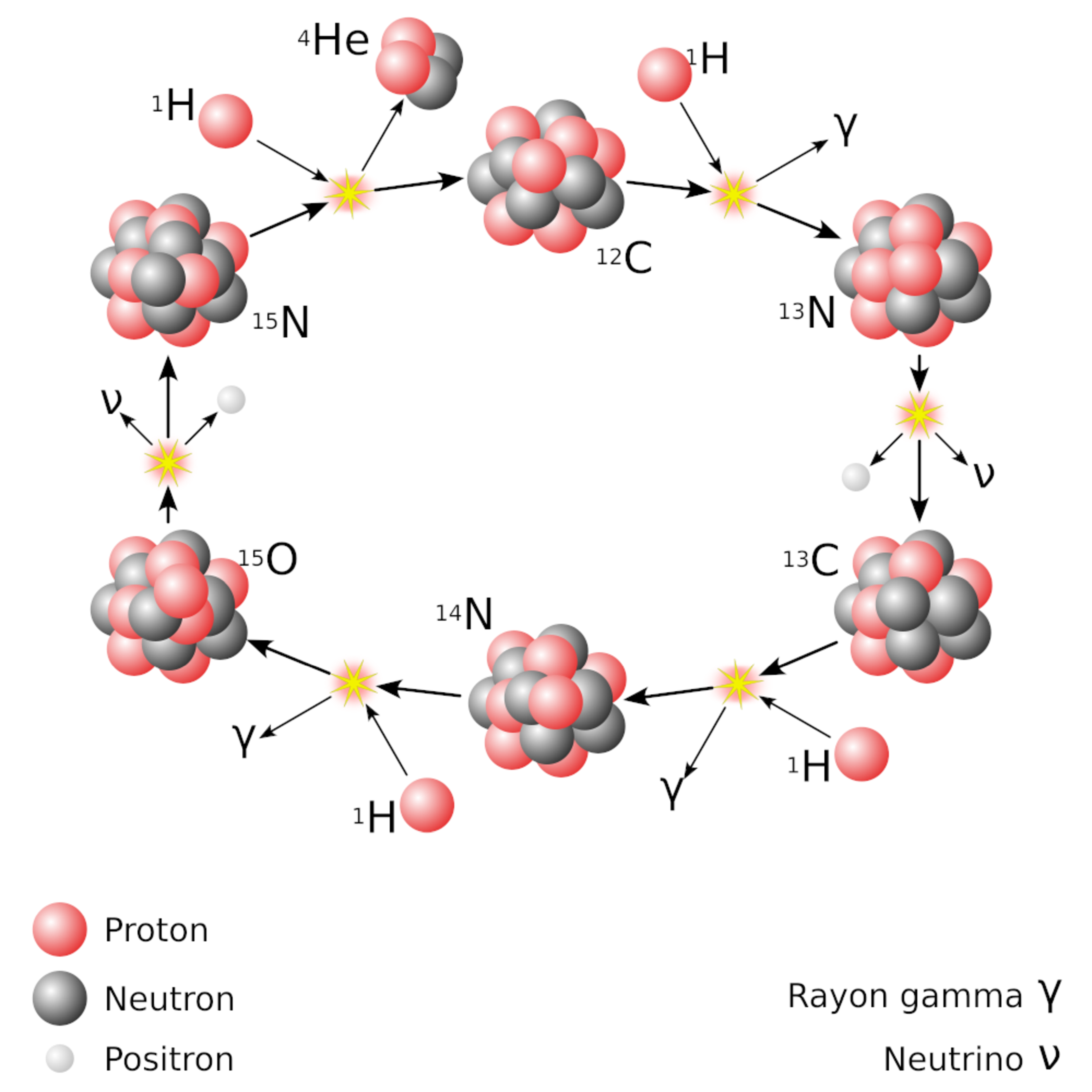
Il existe des variants du cycle CNO. En particulier, la dernière étape peut produire (en moyenne une fois sur 2500) un noyau de \(\ce {^{16}_{8}O}\) :
\begin {align} &\ce {^{15}_{7}N}+\ce {^{1}_{1}H}\rightarrow \ce {^{16}_{8}O}+\gamma \end {align}
Ce noyau va lui-même subir différentes transformations, avec, in fine, la synthèse de \(\ce {^{4}_{2}He}\) et de \(\ce {^{14}_{7}N}\), lequel retourne dans le cycle CNO initial. Par conséquent, le cycle CNO modifie les proportions de carbone, d’oxygène, et d’azote dans le coeur de l’étoile. En régime stationnaire, \([\ce {^{12}_{6}C}]/[\ce {^{13}_{6}C}]\approx 3.5\) et \(\ce {^{14}_{7}N}\) devient le noyau majoritaire étant donné le caractère limitant de sa fusion avec un proton.
Les étoiles « évoluées » (qui ont brûlé l’hydrogène de leur coeur)19 peuvent fusionner des éléments de plus en plus lourds jusqu’à synthétiser du fer, noyau le plus stable.
La fusion de deux particules \(\alpha \) (\(\ce {^{4}_{2}He}\)) produit un noyau de \(\ce {^{8}_{4}Be}\) très instable (demie-vie \(8.2\times 10^{-17}\)s) qui se désintègre en noyaux légers sauf s’il fusionne dans l’intervalle avec une troisième particule \(\alpha \). Cette capture produit un noyau de \(\ce {^{12}_{6}C}\) dans un état excité connu sous le nom d’état de Hoyle, qui se désintègre généralement en trois nouvelles particules \(\alpha \), mais relaxe environ une fois sur 2400 vers l’état fondamental (stable) de \(\ce {^{12}_{6}C}\). La température au centre de l’étoile doit donc dépasser \(T\approx 100\times 10^6\)K afin que la fusion des particules \(\alpha \) soit suffisamment rapide pour produire des quantités significatives de carbone selon cette réaction « triple \(\alpha \) » (Fig. 1.8) :
\begin {align} &\ce {^{4}_{2}He}+\ce {^{4}_{2}He}\rightarrow \ce {^{8}_{4}Be}&(-91.8\mathrm {\ keV}) \nonumber \\ &\ce {^{8}_{4}Be}+\ce {^{4}_{2}He}\rightarrow \ce {^{12}_{6}C}+2\gamma &(+7.367\mathrm {\ MeV}) \end {align}
La réaction triple \(\alpha \) libère donc \(7.275\)MeV. Certains des noyaux de \(\ce {^{12}_{6}C}\) synthétisés peuvent par ailleurs fusionner avec une particule \(\alpha \) supplémentaire pour produire de l’oxygène :
\begin {align} &\ce {^{12}_{6}C}+\ce {^{4}_{2}He}\rightarrow \ce {^{16}_{8}O}+\gamma &(+7.162\mathrm {\ MeV}) \end {align}
Il est remarquable que la synthèse du carbone ne soit rendue possible que par la (quasi-) résonnance entre l’état fondamental de \(\ce {^{8}_{4}Be}\) et l’état de Hoyle de \(\ce {^{12}_{6}C}\) qui favorise la capture d’une troisième particule \(\alpha \) pendant la durée de vie très courte du premier. Sans cette résonance, le rendement de la nucléosynthèse du carbone serait trop faible pour expliquer son abondance dans l’univers.
Les réactions de fusion peuvent se poursuivre jusqu’au fer si la masse de l’étoile, donc la température que peut atteindre le coeur le permet. La fusion du carbone démarre à \(T=10^9\)K, et produit du sodium, du néon et du magnésium 23 :
\begin {align} &\ce {^{12}_{6}C}+\ce {^{12}_{6}C}\rightarrow \ce {^{23}_{11}Na}+\ce {^{1}_{1}H} \nonumber \\ &\ce {^{12}_{6}C}+\ce {^{12}_{6}C}\rightarrow \ce {^{20}_{10}Ne}+\ce {^{4}_{2}He} \nonumber \\ &\ce {^{12}_{6}C}+\ce {^{12}_{6}C}\rightarrow \ce {^{23}_{12}Mg}+\ce {^{1}_{0}n} \end {align}
La dernière réaction domine au delà de \(T=1.1\times 10^9\)K. Passé \(T=1.2\times 10^9\)K, les noyaux de néon peuvent soit se photo-désintégrer, soit fusionner avec une particule \(\alpha \) :
\begin {align} &\ce {^{20}_{10}Ne}+\gamma \rightarrow \ce {^{16}_{8}O}+\ce {^{4}_{2}He} \nonumber \\ &\ce {^{20}_{10}Ne}+\ce {^{4}_{2}He}\rightarrow \ce {^{24}_{12}Mg}+\gamma \end {align}
A ce stade, la fusion des isotopes du carbone et du néon avec des particules \(\alpha \) produit également des neutrons :
\begin {align} &\ce {^{13}_{6}C}+\ce {^{4}_{2}He}\rightarrow \ce {^{16}_{8}O}+\ce {^{1}_{0}n} \nonumber \\ &\ce {^{22}_{10}Ne}+\ce {^{4}_{2}He}\rightarrow \ce {^{25}_{12}Mg}+\ce {^{1}_{0}n} \end {align}
Ces neutrons peuvent être capturés par d’autres noyaux qui voient leur nombre de nucléons augmenter (processus « \(s\) »). Les neutrons excédentaires finissent par se transformer en proton (désintégration \(\beta ^-\) avec émission d’un électron et d’un neutrino). Tous les éléments jusqu’au Bismuth 209 peuvent en principe être synthétisés par le processus \(s\). Si la température dépasse \(T=2\times 10^9\)K, l’oxygène fusionne et produit différents nucléides. Les cinq principales réactions sont :
\begin {align} &\ce {^{16}_{8}O}+\ce {^{16}_{8}O}\rightarrow \nonumber \ce {^{28}_{14}Si}+\ce {^{4}_{2}He} \\ &\ce {^{16}_{8}O}+\ce {^{16}_{8}O}\rightarrow \ce {^{31}_{15}P}+\ce {^{1}_{1}H} \nonumber \\ &\ce {^{16}_{8}O}+\ce {^{16}_{8}O}\rightarrow \ce {^{31}_{16}S}+\ce {^{1}_{0}n} \nonumber \\ &\ce {^{16}_{8}O}+\ce {^{16}_{8}O}\rightarrow \ce {^{30}_{14}Si}+2\ce {^{1}_{1}H} \nonumber \\ &\ce {^{16}_{8}O}+\ce {^{16}_{8}O}\rightarrow \ce {^{30}_{15}P}+\ce {^{2}_{1}D} \end {align}
Les particules \(\alpha \), protons et neutrons libérés peuvent être capturés par d’autres noyaux et former chlore, argon, potassium, calcium, titane, ... Enfin, au delà de \(T=3\times 10^9\)K, une partie du silicium est photo-désintégrée ; les produits de cette désintégration peuvent fusionner avec le silicium lui-même pour former tous les éléments jusqu’au fer 56, noyau le plus stable. L’étoile n’a plus alors que quelques jours à vivre. Son coeur de fer, dégénéré et thermonucléairement inerte, va s’effondrer sous son propre poids et l’onde de choc qui s’ensuit va disperser ses couches supérieures (supernova de type II).
Une partie des éléments au-delà du fer sont synthétisés au coeur des étoiles par le processus \(s\) décrit ci-dessus (\(s\) pour « slow », capture lente de neutrons). Lors de l’effondrement du coeur de fer d’une étoile massive, les protons capturent les électrons pour former une « étoile à neutrons » (voir un « trou noir », cf. chapitre 3). Un grand nombre de ces neutrons vont être dispersés par l’onde de choc et absorbés par les éléments légers (processus « \(r\) » plus rapide que la désintégration \(\beta ^-\)) pour produire les éléments (et leurs isotopes) les plus lourds. Toutefois, l’abondance des éléments tels que l’or, l’uranium et bien d’autres ne saurait être expliquée par les seules supernovas de type II. Ils proviennent plus vraisemblablement de processus \(r\) consécutifs à la collision d’étoiles à neutrons. En particulier, l’abondance de ces élements dans le système solaire suggère qu’une telle collision a eu lieu dans le voisinage de la nébuleuse protostellaire du Soleil peu avant sa naissance.
1.La limite thermodynamique est la limite \(N,\,V\to \infty \) à \(n=N/V\) constant, où le gaz pourra être caractérisé par sa température \(T\), sa densité \(n\), et sa pression \(P\). Dans cette limite, les descriptions micro-canonique, canonique et grand-canonique sont équivalentes.
2.\(\Gamma (\alpha +1)=\alpha \Gamma (\alpha )\) par parties et \(\Gamma (\tfrac {1}{2})=\sqrt {\pi }\).
3.On suppose ces collisions élastiques (pas de transfert de chaleur), en accord avec la définition thermodynamique de la pression.
4.Le calcul de la pression thermodynamique du paragraphe 1.2.2 ne tient pas compte du principe d’exclusion de Pauli (les vecteurs \(\vec {k}_i\) et les états de spin doivent être tous différents). A l’ordre 0 en température (\(T\to 0\)), seul l’état fondamental d’un gaz dégénéré est accessible indépendemment de son volume, si bien que la pression thermodynamique est simplement :
\begin {equation} P=-\left (\frac {\partial E}{\partial V}\right )_{S,N}=-\left (\frac {\partial E}{\partial V}\right )_{N}\,. \nonumber \end {equation}
En écrivant \(E\propto N^{5/3}V^{-2/3}\), on retrouve aisément la pression cinétique.
5.La longueur de de Broglie est également comparable à l’extension d’un paquet d’ondes Gaussien d’énergie \(\varepsilon =\tfrac {3}{2}kT\) (ne serait-ce que pour de simples raisons dimensionelles!). Il est donc d’usage de dire que « le gaz dégénère quand les fonctions d’ondes des électrons thermiques commencent à se recouvrir ».
6.En effet, la température affecte marginalement la distribution des particules loin du potentiel chimique. Voir les développements de Sommerfeld pour une démonstration au delà de l’ordre 0 en température du paragraphe 1.2.3.
7.On traite ici par analogie les photons comme les fermions au paragraphe 1.2 ; toutefois, les photons n’ont pas d’interactions entre eux et ne peuvent donc se thermaliser que par couplage avec de la matière. Ces mécanismes de couplage seront explicités au chapitre 2.
8.On peut utiliser la fonction de Riemann ou la transformation de Mellin pour montrer que :
\begin {equation} \int _0^\infty dx\,\frac {x^3}{e^x-1}=\frac {\pi ^4}{15}\,. \nonumber \end {equation}
9.Ce rayonnement est par nature « invisible » d’un observateur à la même température puisqu’il constitue le bruit de fond photonique ; il n’est clairement séparable de ce bruit de fond que dans une situation hors-équilibre global où une source à la température \(T\) est observée par un détecteur à la température \(T^\prime \ne T\). C’est le cas par exemple lorsque le Soleil, assimilable à un corps noir de température \(T=5775\) K, est observé depuis la Terre à \(T^\prime =300\) K, les photons solaires ayant subi peu d’interactions sur leur trajet (voir paragraphe 1.3.4).
10.On peut aussi calculer la pression à partir d’une approche thermodynamique analogue à celle du paragraphe 1.2.2.
11.Il s’agit d’une température effective de couleur plutôt que de la température réelle de la « surface » du Soleil (voir définition de la photosphère au chapitre 2). On suppose que tous les photons émis au coeur du Soleil sont thermalisés à la température \(T_\odot \) une fois parvenus à sa surface.
12.La définition normalisée de la luminosité solaire est \(L_\odot =3.828\times 10^{26}\) W.
13.On suppose ici la surface \(A\) perpendiculaire à l’axe qui la relie à l’étoile ; dans le cas contraire il faut lui substituer la surface effective \(A\cos \theta \), où \(\theta \) est l’angle que fait la normale à la surface avec cet axe.
14.Cette condition est bien plus stricte que d’imposer la stationnarité de \(\rho (\vec {r})\) (divergence des courants de matière nulle). En effet, la pression cinétique dans un objet parcouru par des courants de matière n’est plus isotrope, aussi cet objet doit-il être décrit par un modèle hydrodynamique (Navier-Stokes). Les corrections hydrodynamiques à la physique d’une étoile (rotation différentielle des gaz, mouvements de convection...) sont quantitatives, mais rarement qualitatives.
15.Autrement dit, la relation \(z_3=\alpha _3R\) qui lie le rayon \(R\) à la densité centrale \(\rho (0)\) conserve l’intégrale \eqref{eq:MRpolytrope}.
16.L’énergie potentielle interne de pesanteur du Soleil, assimilé à une sphère homogène de rayon \(R_\odot =696\,340\) km et de masse \(M_\odot =2\times 10^{30}\) kg, est \(U_\odot =-3GM^2/(5R)=-2.3\times 10^{41}\) J [Eq. \eqref{eq:Ugsphere}]. En supposant que la totalité de cette énergie potentielle gagnée par la contraction du nuage de gaz protostellaire a été convertie en rayonnement avec une luminosité constante \(L_\odot =3.828\times 10^{26}\) W, l’âge du Soleil serait \(T=U_\odot /L_\odot =19\times 10^6\) ans – bien inférieur à l’âge géologique de la Terre notamment. Cette contradiction démontre l’existence d’une source d’énergie additionnelle à l’intérieur de l’étoile.
17.Si sa masse est inférieure à la masse de Chandrashekar \eqref{eq:Chandrasekhar}, sinon elle s’effondre complètement sous son propre poids. Voir le chapitre 3 pour une discussion de l’évolution des étoiles et de leur devenir quand le combustible des réactions nucléaires est épuisé.
18.Ces neutrinos interagissent peu avec la matière et ne contribuent donc pas au chauffage et à la luminosité de l’étoile.
19.La fusion dans les étoiles évoluées se poursuit généralement « en couches » : Le coeur brûle du carbone par exemple tandis que la fusion de l’hélium et de l’hydrogène continue (démarre, en fait) dans des coquilles périphériques où la température s’est suffisamment élevée pour le permettre. Si le coeur n’est pas convectif (voir chapitre 2), il y a en effet peu de brassage des combustibles/produits de fusion entre ces différentes couches.